Performance di sistemi paralleli e concorrenti

Latenza e throughput

In termini generali, in un sistema informatico le due grandezze di maggior interesse per misurare le prestazioni sono la latenza e il throughput. La latenza consiste nella capacità del computer di rispondere il più velocemente possibile ad una richiesta, e si misura in secondi. Il throughput invece è la capacità del computer di soddisfare il maggior numero possibile di richieste per unità di tempo, e si misura in operazioni/secondo. 

Queste due grandezze sono legate a due esigenze differenti:

– la latenza è legata all’esperienza del singolo utente o comunque a quanto il sistema è veloce nel rispondere alla singola richiesta;

– il throughput indica invece più una efficienza generale del sistema, inteso come capacità di soddisfare il maggior numero di utenti per unità di tempo.

La latenza è una caratteristica di performance particolarmente apprezzabile nei sistemi dove l’utente è l’utilizzatore del calcolatore: sistemi desktop, mobile o siti web. Il throughput è apprezzato invece quando il punto di vista è quello del committente di un sistema informatico: ad esempio una banca (il numero di utenti soddisfatti per unità di tempo è più importante dell’occasionale lentezza di una singola attività) o una società di telecomunicazioni (il numero di utenti connessi è più importante di qualche occasionale disconnessione). Sono due grandezze che sono entrambe direttamente coinvolte sia dalla parallelizzazione che dalla concorrenza. Ad esempio un computer con una gestione migliore della concorrenza (ad esempio 8 processori in parallelo anzichè 4) riesce a soddisfare più velocemente sia le singole richieste che il throughput generale. 

Tuttavia sono due aspetti diversi delle performance che possono essere influenzati per garantire o l’una o l’altra. Ad esempio un sistema operativo molto aggressivo sui processi in stato waiting può puntare a “liberare risorse” per rendere più efficace il singolo processo in primo piano, migliorandone i tempi di latenza. E’ tuttavia poco efficiente in quanto i processi in background potrebbero richiedere molto tempo per essere svolti. E’ il caso dei sistemi operativi desktop, che danno importanza alla latenza.

Viceversa in un sistema server che serve più processi, la singola richiesta può essere rallentata in caso di molti processi attivi, perchè questo diminuisce le risorse a disposizione del singolo processo, anche se il throughput complessivo può aumentare considerevolmente. I sistemi server danno importanza al throughput.

Tempo di esecuzione in un sistema concorrente

Ipotizziamo di avere N task in esecuzione su un sistema con C cpu. 

Ciascun task ha un suo tempo di esecuzione T_i ed una priorità P_i (espressa come percentuale di uso totale delle cpu). Si ipotizza poi con Q il tempo del singolo quanto, e CS il tempo di context switch.

La latenza del task i-esimo è quindi:

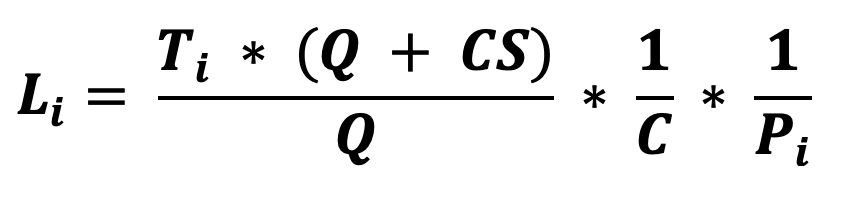
il throughput è dato da:

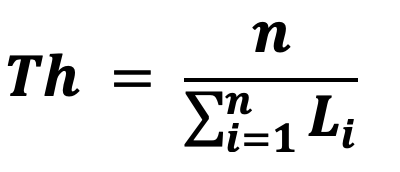
Ad esempio ipotizziamo N=5, C=2, e due task con tempo T=[100, 50] e priorità P = [30, 70].

Si poi Q = 6ms e CS = 0,5ms.

Sarà 

L1= (100*(6+0,5) / 6) * 1/2 * 1/0,3 = 180ms 

L2 = (50*(6+0,5) / 6) * 1/2 * 1/0,7 =  38ms

Il throughput sarà invece = 2 / (0,180+0,038) = 9,17 task/secondo  

Tempo di esecuzione in un sistema parallelo 

Sappiamo che la parallelizzazione riduce il tempo di esecuzione di un task grazie al fatto che questo tempo di esecuzione viene “suddiviso” tra più processori. Tuttavia per la maggior parte dei task non tutto il tempo di esecuzione è parallelizzabile: se un task deve usare una risorsa condivisa, o deve inizializzare un set di dati, viene eseguita una sola sequenza.

Il tempo T  di esecuzione è quindi composto da due parti: una parallelizzabile ed una non. Quindi il tempo totale sarà pari al tempo non parallelizzabile più il tempo parallelizzabile diviso per il numero di CPU.

Dove S è la parte sequenziale (non parallelizzabile) e P quella parallela, ed n il numero di CPU.

Per n=1 avremo: T₁ = S+P (caso monoprocessore)

Per n=2 avremo: T₂ = S+P/2

Per n=3 avremo: T₃= S+P/3

E così via avremo T_n = S+P/n

Legge di Amdahl

Possiamo calcolare il miglioramento M su un sistema con più processori come il rapporto tra il tempo monoporcessore e il tempo con n processori:  

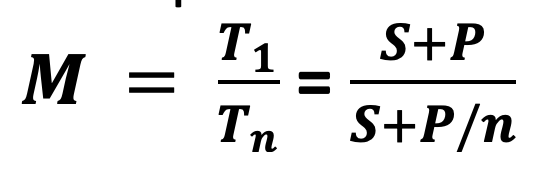
per n molto grande P/n diventa molto piccolo e quindi si può approssimare a (S+P)/S che è un limite asintotico.

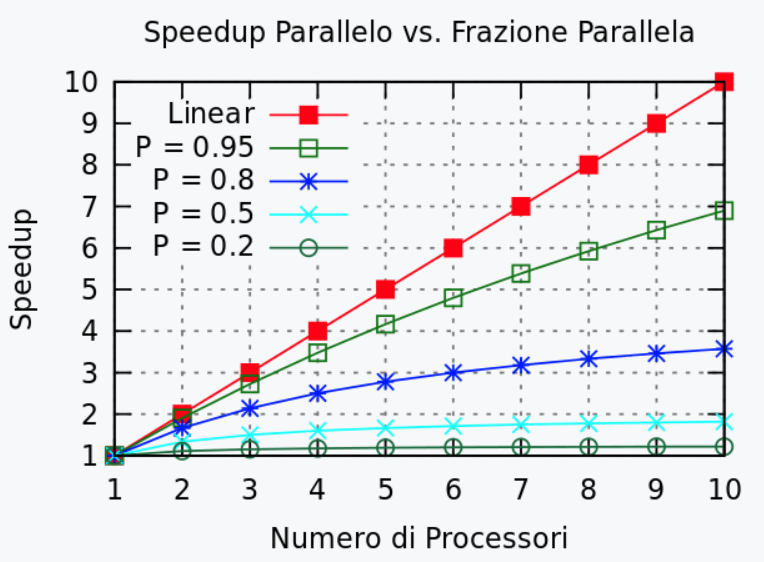
Questa formulazione viene chiamata legge di Amdhal.

Vediamo un esempio numerico.

Ipotizziamo che un task ha S = 10ms e P = 30ms.

Avremo :

T₁ = 10+30 = 40ms e M = 0

T₂ = 10+30/2 = 30ms e M = 40/30=1,33

T₃ = 10+30/3 = 20ms e M = 40/20=2

T_n = 10+30/n ≃ 10 e M = 40/10=4 

Quindi in questo caso con 2 cpu le prestazioni migliorano del 33%, con 3 del doppio, ma anche con infinite cpu al massimo possono migliorare fino a 4 volte. 

Tempo di esecuzione in un sistema concorrente con applicazioni che sfruttano la programmazione parallela.

Combinando la legge di Amdahl con il calcolo del tempo di esecuzione abbiamo quindi:

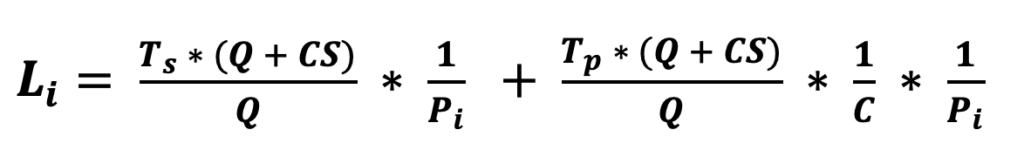
ovvero è la somma del tempo sequenziale (T_s) e del tempo parallelizzabile (T_p).