Funzioni ricorsive
La ricorsione
Le funzioni ricorsive sono una classe di funzioni che prevedono nella loro definizione la chiamata a se stesse.
L’obiettivo di queste funzioni è quello di semplificare o suddividere il set di dati ricevuti come parametro e richiamare se stesse con un set di dati semplificato/ridotto, fino ad arrivare ad un caso base. La tecnica viene chiamata ricorsione e gli algoritmi che la utilizzano sono chiamati ricorsivi.
La struttura di una funzione ricorsiva è determinata da una condizione:
1) caso base: se il parametro di input rispetta determinati requisiti, allora la funzione svolge il suo compito e restituisce quando previsto un risultato;
2) caso generale: se non rispetta i suddetti requisiti, la funzione chiama se stessa con parametri opportunamente modificati.
Nel diagramma sottostante uno schema di funzionamento generale di una funzione che chiama se stessa più volte fino ad arrivare ad un caso base.
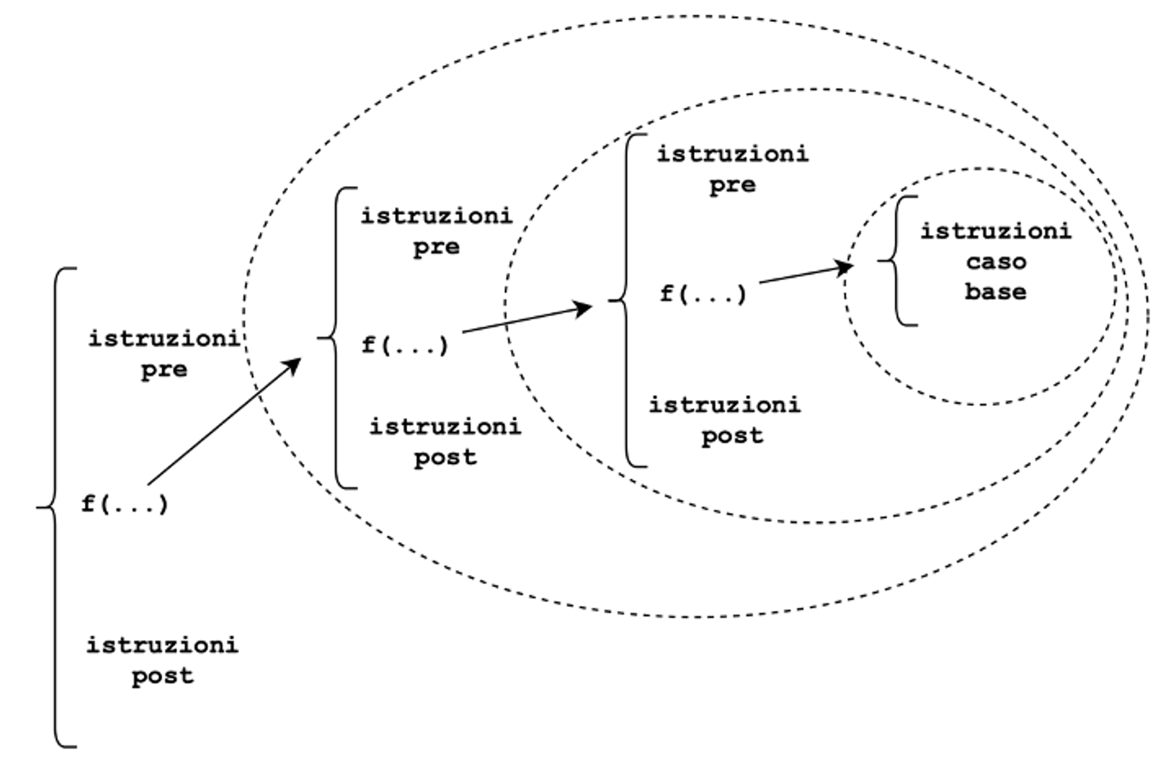
Ambiti di applicazione
Gli algoritmi ricorsivi offrono in generale una soluzione più sintetica ed elegante a problemi che prevedono cicli, in quanto non richiedono di usare variabili per gestire contatori o indici, quindi è possibile separare ogni ciclo in funzioni separate. Questo permette di semplificare problemi complessi in problemi più semplici, più semplicid da programmare, ed in alcuni casi anche sfruttare la programmazione parallela (su più cpu) per risolverli più velocemente.
La loro principale limitazione è che siccome le funzioni usano lo stack, un numero elevato di chiamate ricorsive a funzione va a riempirlo con un rischio di errore di “stack overflow”. Inoltre la creazione di una funzione (e la relativa distruzione) richiede tempo macchina col risultato di peggiorare leggermente le prestazioni (rispetto alla soluzione iterativa).
Questa problematica, importante ancora nell’uso di sistemi informatici negli anni 70-80, oggi è largamente minimizzata dalla dimensione delle memorie, ed anzi la ricorsione trova vantaggi prestazionali in alcuni casi di utilizzo grazie all’uso di processori multicore e la programmazione parallela.
Vediamone ora qualche esempio.
Fattoriale
Come noto, la funzione f(x) = n! detta anche “fattoriale di n” è definita come
f(x) = n*n-1*n-2*…*1 = n!
Essa è cioè il prodotto di tutti gli interi che vanno da 1 a n. Essa può essere definita in modo ricorsivo in quanto è n! = n*(n-1)!
| Input | Funzione | |
| x=1 | f(x)=1 | Caso base |
| x>1 | f(x)=x * f(x-1) | Caso generale |
Proviamo a svolgere i passaggi per x = 5:
| Input | Esecuzione allo step | Valore calcolato |
| 5 | f(5)= 5* f(4) | 5 * f(4) |
| 4 | f(4)= 4* f(3) | 5 * (4 * f(3)) |
| 3 | f(3)= 3* f(2) | 5 * (4 * (3 * f(2)) |
| 2 | f(2)= 2* f(1) | 5 * (4 * (3 * (2 * f(1))) |
| 1 | f(1)= 1 | 5 * (4 * (3 * (2 * 1))) |
Come si vede dallo svolgimento la funzione è chiama se stessa con un parametro che decresce di 1 fino a quando non si arriva al caso base (1).
Qui una rappresentazione grafica. Si noti che in questo esempio tutte le funzioni sono deterministiche.
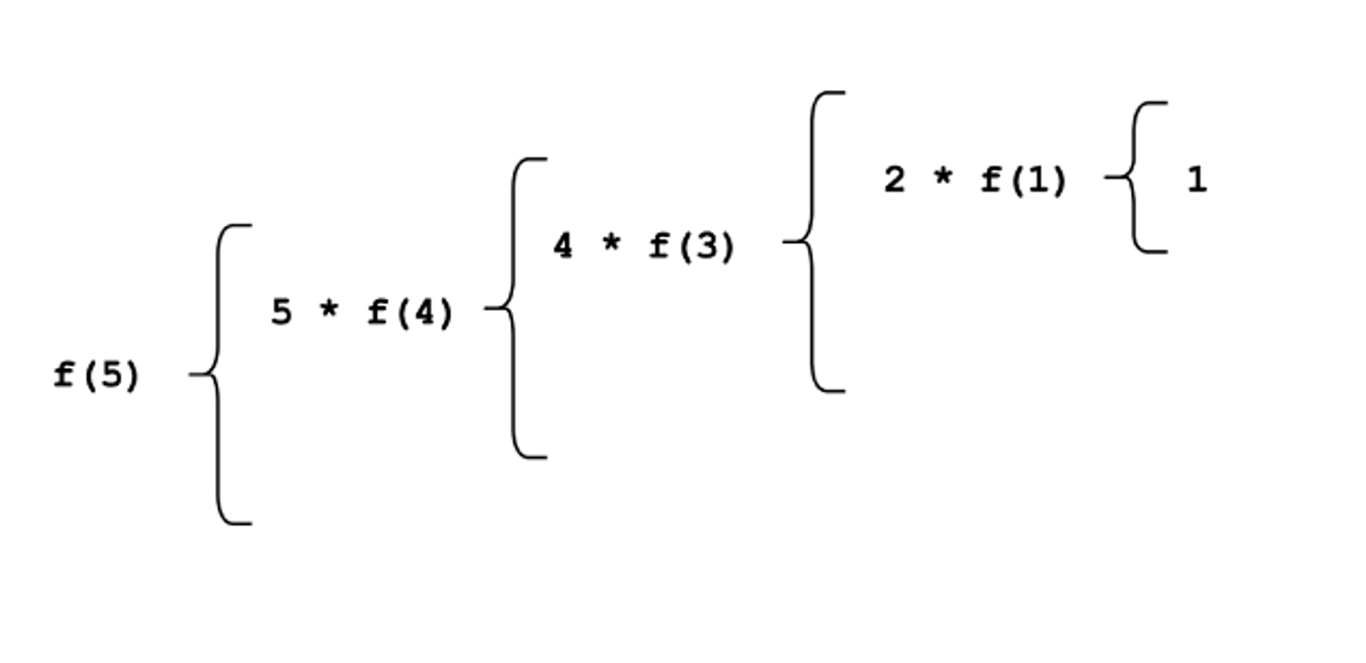
#include <iostream>
using namespace std;
int f(int n) {
if (n==1) {
return 1;
} else {
return n * f(n-1);
}
}Questa tecnica di programmazione viene chiamata anche divide et impera, perché suddivide un problema in sottoproblemi, e li risolve separatamente per poi ricomporli in un problema unico.
Numeri di Fibonacci
Come noto, la serie di Fibonacci è definita dalla seguente funzione generativa:
f(1) -> 1
f(2) -> 2
f(n) -> f(n-1) + f(n-2)
In questo caso quindi la funzione ricorsiva è funzione di due chiamate ricorsive sommate tra loro.
Proviamo a svolgerla per n=5:
| Input | Esecuzione allo step | Valore finale |
| 5 | f(5)= f(4) + f(3) | f(4) + f(3) |
| 4 | f(4)= f(3) + f(2) | (f(3) + f(2)) + f(3) |
| 3 | f(3)= f(2) + f(1) | ((f(2) + f(1)) + f(2)) + (f(2) + f(1)) |
| 2 | f(2)= 1 | ((1 + 1) + 1) + (1 + 1) |
| 1 | f(1)= 1 | 5 |
Qui una rappresentazione grafica.
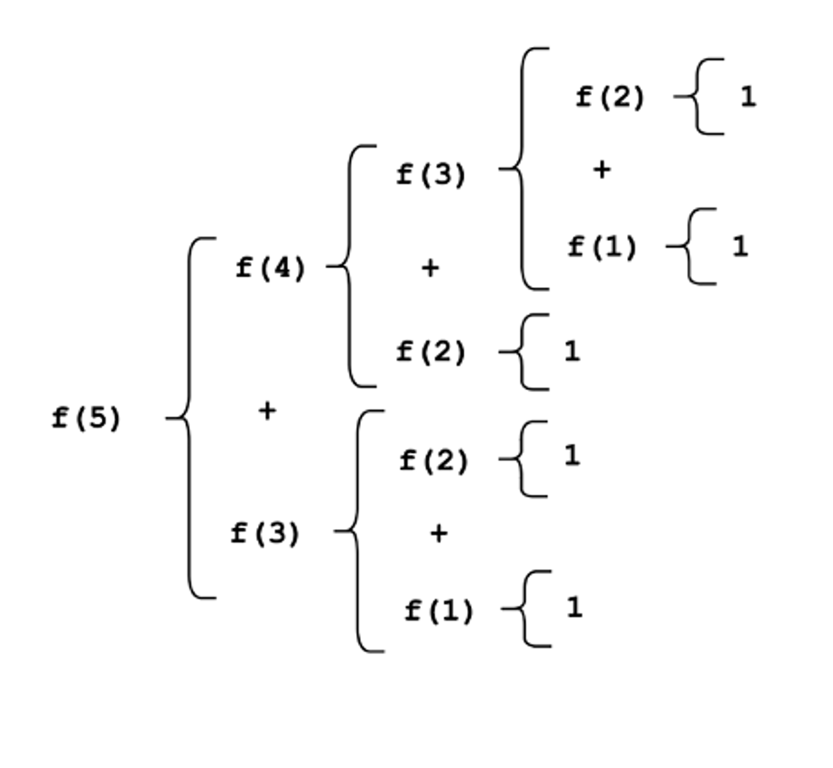
In C++ (si omette il main) si ottiene usando il divide et impera:
int fibo(int n) {
if (n==1) {
return 1;
};
if (n==2) {
return 1;
}
return fibo(n-1) + fibo(n-2);
}Analogamente si può procedere per la generazione di qualsiasi serie. Si può osservare che anche questa funzione è deterministica.
Si può notare tuttavia che prestazionalmente questo tipo di soluzione richiede di norma un tempo esponenzialmente maggiore rispetto ad una soluzione iterativa. Infatti se si richiama la ricorsiva per f(5), questa chiama f(4) e f(3), che a loro volta chiamano f(3) e f(2), e così via, col risultato che ogni chiamata viene svolta molte volte.
Se invece scriviamo questa funzione:
void fibo(int n, int f[]) {
if (n==1) {
f[0]=1;
f[1]=1;
} else {
fibo(n-1, f);
f[n] = f[n-1] + f[n-2];
}In questo caso la funzione ricorsiva dopo aver chiamato se stessa con n-1, va a salvare il risultato nell’array, e quindi ogni livello viene chiamato una sola volta.
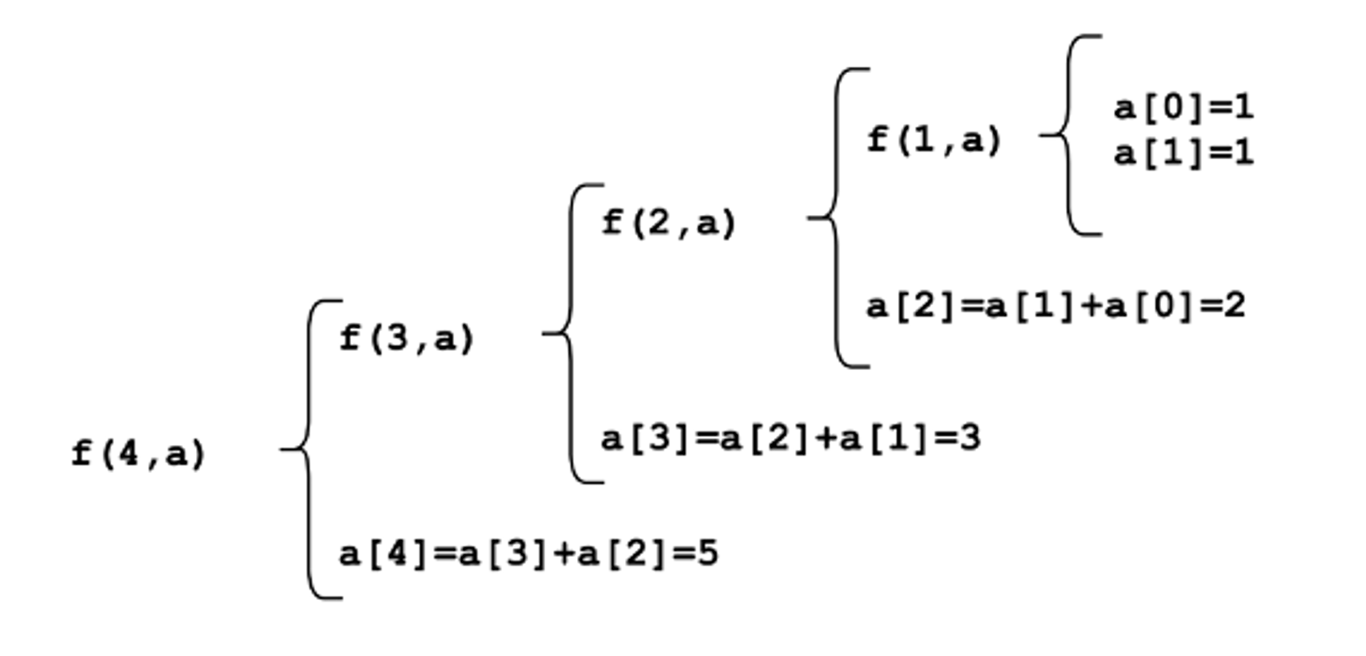
Questa seconda tecnica di programmazione, che utilizza una memoria per “ricordare” i passaggi precedenti, viene chiamata programmazione dinamica.
Verifica di un numero primo
La funzione ricorsiva riceve come parametri il numero da verificare e un divisore e restituisce un valore booleano (true se primo, false se non primo).
Essa ha dunque la seguente firma:
bool f(int numero, int divisore)In questo caso quindi è funzione di due parametri, e la ricorsione avviene variando uno di essi (l’altro è costante).
La possiamo implementare nel seguente modo:
bool isPrime(int n, int d) {
if (d == 1) {
return true;
}
if (n % d == 0) {
return false;
} else {
return isPrime(n, d-1);
}
}Vediamo in dettaglio come funziona:
- Se d==1, è il caso base, abbiamo esaurito tutti i divisori;
- Se n%d==0, è un altro caso base, il numero non è primo, non serve continuare;
- in tutti gli altri casi, si testa la funzione riducendo di 1 il divisore.
La funzione viene richiamata con
isPrime(n, n-1)Proviamo a vedere un esempio con n = 5:
| Input (n, d) | chiamata ricorsiva |
| (5,4) | -> f(5,3) |
| (5,3) | -> f(5,2) |
| (5,2) | -> f(5,1) |
| (5,1) | true |
Graficamente:
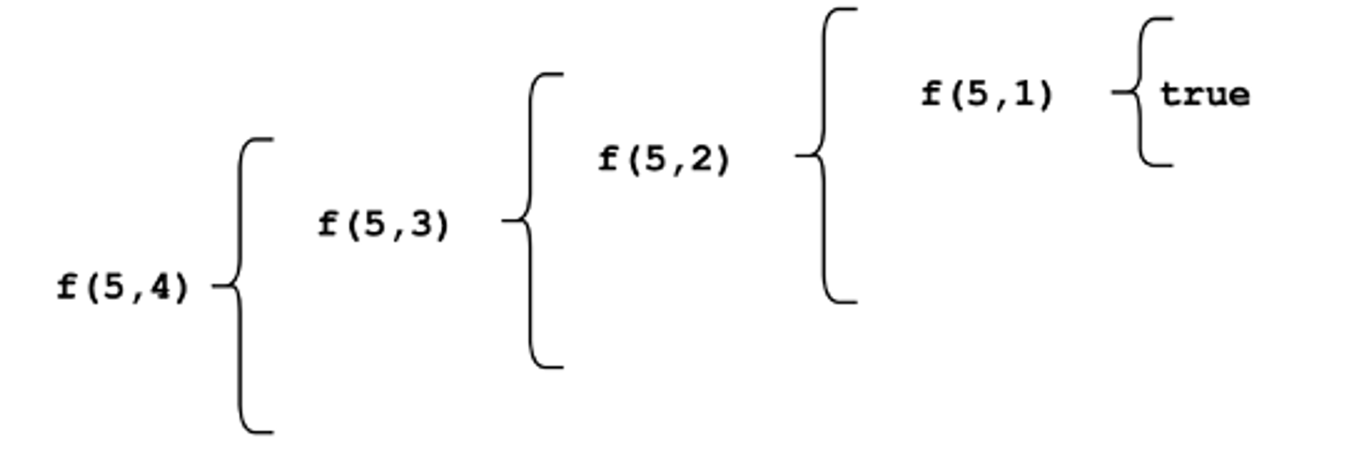
Ora un esempio con n=10 che restituisce false.
| Input (n, d) | hiamata ricorsiva |
| (10,9) | f(10,8) |
| (10,8) | f(10,7) |
| (10,7) | f(10,6) |
| (10,6) | f(10,5) |
| (10,5) | false |
