Algoritmi di ordinamento in C/C++
Premessa
Un algoritmo di ordinamento è una tipologia di algoritmo che prende come input un array di elementi non ordinati e li ordina secondo un criterio di ordinamento prestabilito, detto “relazione d’ordine“. Ad esempio una relazione d’ordine può essere l’ordine crescente dei numeri, oppure l’ordine alfabetico delle stringhe, oppure ancora in base a regole più complesse che tengono conto di diversi fattori.
Gli algoritmi di ordinamento sono una applicazione informatica di primaria importanza ed è considerata una operazione di base per la maggior parte delle operazioni di calcolo numerico sia in ambito scientifico che economico ed industriale. Nella storia dell’informatica ha avuto una tale importanza che in alcune lingue la parola “computer” viene tradotta come “ordinatore” (ad esempio francese o spagnolo).
Di norma tutti gli algoritmi di ordinamento operano mediante operazioni di confronto tra due elementi dell’array, ed attuano meccanismi di scambio tra coppie di valori secondo la relazione d’ordine.
In questa lezione vedremo quattro algoritmi di ordinamento molto noti e significativi. Come riferimento del data set da ordinare useremo un array di numeri interi da ordinare secondo una relazione d’ordine di numeri crescenti. Gli algoritmi hanno comunque portata generale e possono essere usati per qualsiasi tipo di dato ordinabile e con qualsiasi relazione d’ordine.
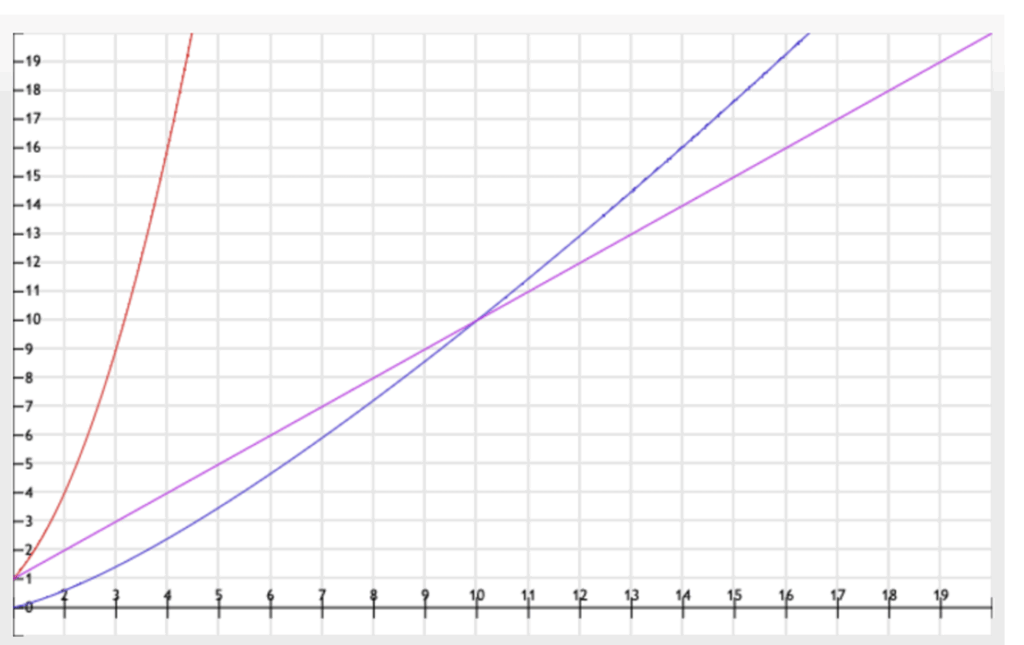
Perché la necessità di realizzare tanti algoritmi? In generale la necessità di sviluppare algoritmi più efficaci ha come obiettivo ottenere prestazioni migliori, ovvero con complessità computazionale minore. Per continuare quindi è necessario conoscere bene cosa è la complessità.
BubbleSort
Questo algoritmo è molto semplice e si basa sul principio di eseguire un ciclo su ogni elemento dell’array. Questo elemento viene confrontato con tutti gli altri elementi, e se necessario scambiato in base alla relazione d’ordine. Quindi in pratica il primo elemento viene confrontato prima col secondo, poi col terzo e così via. Ogni volta che il confronto da esito negativo, l’elemento corrente viene scambiato con quello esaminato.
Si tratta quindi realizzare un ciclo esterno e su questo un ciclo interno.
Un esempio in grafica di ogni ciclo interno.
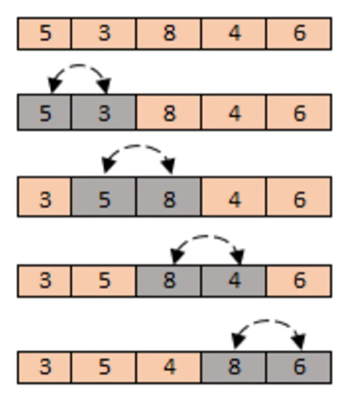
Qui un esempio C++ con un array di interi ordinato in modo crescente.
void bubbleSort(int list[], int n) {
for (int i=0; i<n-1; i++) { // prendo ogni elemento
for (int j=i+1; j<n; j++) { //e lo confronto con ogni altro elemento
if (list[i]>list[j]) { // se serve
swap(list[i], list[j]); // li scambio
}
}
}
}Il comportamento è proprio come quello di una “bolla” dove l’elemento più “leggero” va verso l'”alto”.
Insertion sort
Si basa sul principio di creare progressivamente un array ordinato nella parte iniziale (“sinistra”) dell’array a partire dal primo elemento.
Si prende l’elemento più a sinistra dell’insieme rimanente (all’inizio tutto l’array) e lo si confronta con gli altri, in modo da inserirlo in modo corretto nella porzione di array già ordinata. Così via con le posizioni successive. Alla fine si ottiene un array ordinato. Qui sotto una immagine coi vari passaggi:

Il codice in C++.
void insertionSort(int list[], int n) {
int i;
int j;
int k;
for (i = 0; i < n-1; i++) { // i è l'indice del primo elemento da ordinare
k = i; // k è l'elemento i-esimo, con
for (j = i+1; j < n; j++) { // notare che il confronto è con l'elemento j=i+2
if (list[j] < list[k]) {
k = j; // se list[k] > list[j], allora k diventa l'elemento j-esimo
}
}
int minimo = list[k];
list[k] = list[i]; // list [k] diventa list [i+1]
list[i] = minimo; // e list[i] diventa il valore più basso tra list[j] e list[i]
}
}Merge sort
Questo algoritmo utilizza la tecnica del “divide et impera” (ovvero semplificare un problema più complesso in problemi più semplici), quindi attraverso la ricorsione.
Ogni step ricorsivo ha quindi un caso generale che funziona nel seguente modo:
– si partiziona l’array in due metà;
– si chiama l’algoritmo ricorsivamente per ciascuna metà (fino al caso base, con array di dimensione 1);
– dopo la chiamata si esegue una funzione apposita di merge (“fusione”) che unisce le due metà ordinando gli elementi.
Qui un esempio che riassume l’algoritmo.
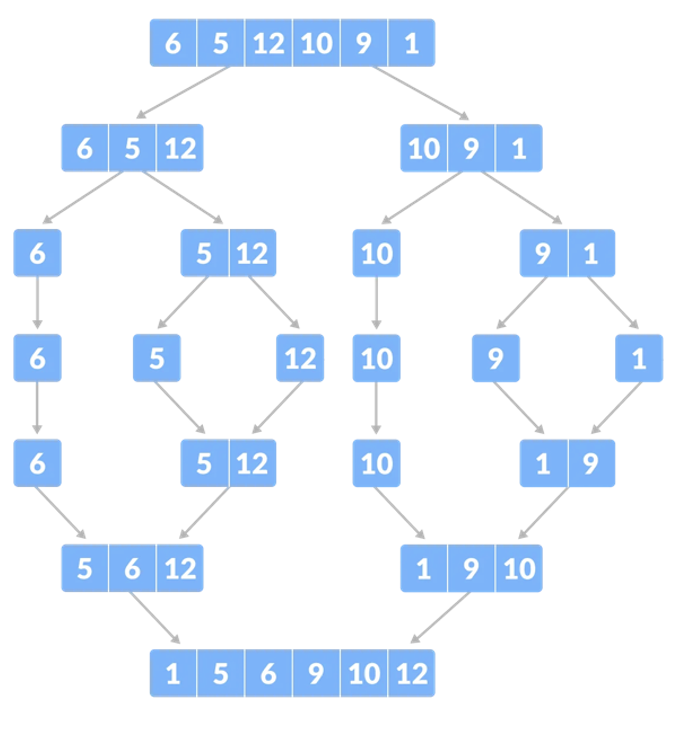
In C++ sono quindi previste due funzioni. Qui il mergeSort ricorsivo:
void mergeSort(int list[], int start, int end) {
int n = end-start;
if (n > 0) {
int center = (end+start)/2;
mergeSort(list, start, center); // si divide la metà sinistra
mergeSort(list, center+1, end); // si divide la metà destra
merge(list, start, center, end); // si esegue il merge
}
}
che come si vede richiama la funzione merge:
void merge(int list[], int start, int center, int end) {
int i = start;
int j = center+1;
int k = 0;
int temp[end-start+1];
while (i<=center && j<=end) { // finchè rimangono elementi in entrambe le metà
if (list[i] <= list[j]) { // inserisco quello più piccolo nel confronto
temp[k] = list[i];
i++; // e incremento l'indice corrispondente (metà sx)
} else {
temp[k] = list[j];
j++; // e incremento l'indice corrispondente (metà dx)
}
k++;
}
while (i<=center) { // aggiungo i rimanenti di sx
temp[k]=list[i];
i++;
k++;
}
while (j<=end) { // aggiungo i rimanenti di dx
temp[k]=list[j];
j++;
k++;
}
for (int z=start; z<=end; z++) {
list[z] = temp[z-start];
}
}
La funzione merge comprende i seguenti passaggi:
– si crea un array temporaneo di merge;
– nel primo step si scorrono le due metà con due indici i e j (che vanno confrontate);
– si confrontano gli elementi e si inserisce quello più piccolo dal confronto;
– si inseriscono poi gli elementi rimanenti (se ci sono) della metà di sinistra;
– si inseriscono infine gli elementi rimanenti (se ci sono) della metà di destra;
– si ricopia l’array temporaneo nella porzione di array principale.
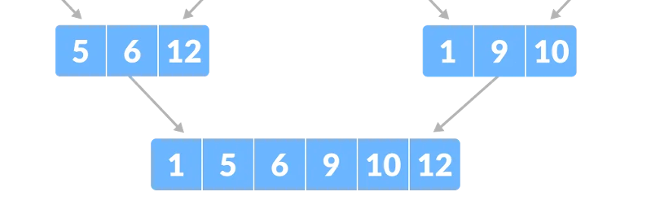
Qui un estratto dell’immagine sopra che mostra un esempio di merge.
Quicksort
L’algoritmo quicksort utilizza anch’esso il divide et impera.
– nel caso generale si individua un elemento dell’array, detto “pivot”;
– si confronta ciascun elemento della prima metà dell’array e lo si scambia se “maggiore” col pivot, tenendo traccia della nuova posizione del pivot;
– si effettua la stessa operazione con la seconda metà, in questo caso si fa lo scambio se “minore” del pivot.
– alla fine si ottengono due partizioni (non necessariamente uguali): quella di sinistra con tutti i valori inferiori al pivot, quella a destra con tutti i valori superiori.
– l’algoritmo richiama se stesso su ciascuna metà, fino a dimensione 1.
Qui una figura che esemplifica i passaggi.
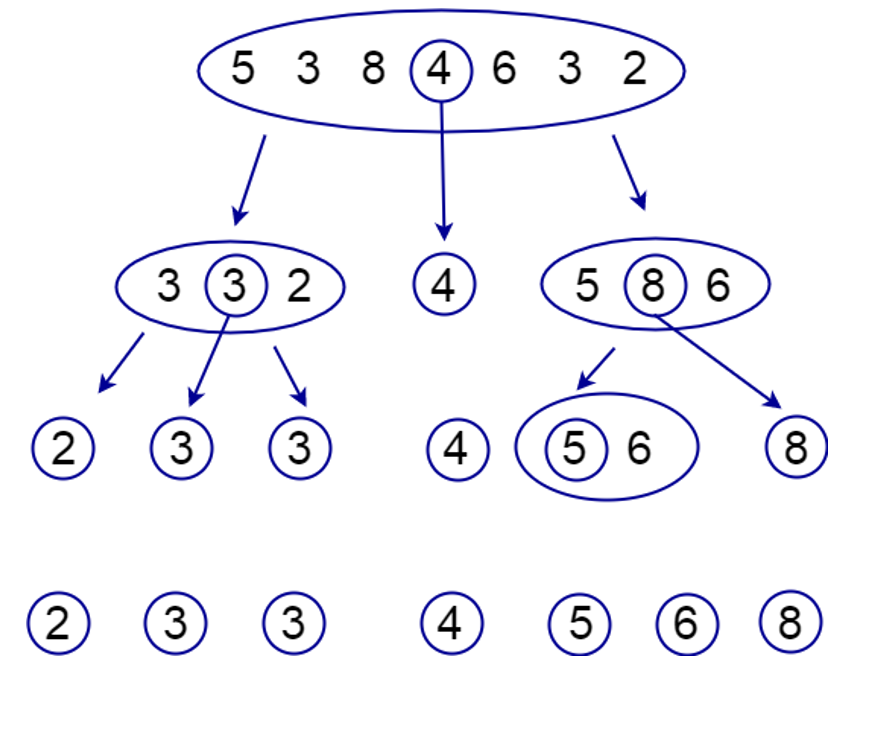
In C++.
void quickSort(int list[], int start, int end) {
if (end - start > 1) { // se il sottoinsieme è più grande di 1
int center = (end+start)/2;
int pivot = list[center]; // trovo l'elemento medio
for (int i=start; i<=end; i++) {
if (i<center) {
if (list[i] > pivot) {
swap(list[i], list[center]);
center=i;
i=start;
}
} else {
if (list[i] < pivot) {
swap(list[i], list[center]);
center=i;
i=start;
}
}
}
quickSort(list, start, center); // eseguo lo stesso algorimto per la metà sx
quickSort(list, center+1, end); // e dx
}
}
Ordinamento e complessità
Come facile immaginare gli algoritmi più semplici sono in genere più lenti. Va comunque anche considerato che un array parzialmente ordinato agevola alcuni algoritmi. Quindi una tabella riassuntiva con le velocità degli algoritmi nella situazione migliore e peggiore.
| Ordinamento | Caso migliore | Caso medio |
| Bubble sort | O(n2) | O(n2) |
| Insertion sort | O(n) | O(n2) |
| Merge sort | O(nlog(n)) | O(nlog(n)) |
| Quick sort | O(nlog(n)) | O(nlog(n)) |