Metodi di programmazione
Cosa è lo sviluppo del software?
Aldilà dell’ovvia risposta, occorre comprendere che sviluppare software consiste nel realizzare una attività artigianale supportata da strumenti software ed un insieme di metodologie ingegneristiche. Grazie a questi tre fattori combinati il programmatore (o il team di sviluppo) riesce a realizzare applicazioni software dalle più semplici alle più complesse, con molti moduli e componenti che interagiscono tra loro per fornire servizi e calcoli all’utente.
Non esiste una procedura meccanica, una metodologia sempre identica per risolvere qualunque tipo di problema. Ogni problema infatti richiede una soluzione specifica, un procedimento particolare che porta ad una determinata sequenza di istruzioni che risolvono quel determinato problema. Ad esempio la procedura per creare un programma che calcola il minimo comune multiplo è certamente molto diversa dalla procedura per creare un programma che calcola il pi greco.
La realizzazione di un programma è quindi “un’arte” che combina creatività, tecnica e metodologie, e la soluzione è a tutti gli effetti una invenzione artigianale.
In questa lezione vedremo diversi strumenti di ragionamento e di metodologia a supporto di questo processo. Resta fondamentale capire che la capacità di produrre creativamente programmi si sviluppa principalmente con l’esercizio continuo: è tramite la pratica costante che si sviluppa quell’elasticità mentale che rende possibile affrontare un sempre maggior numero di problemi e trovare una soluzione. Dopo aver scritto tanto software, visto tanti problemi, la mente riesce ad avere quel livello sufficiente di allenamento che le permette di collegare automaticamente le proprie esperienze con la propria capacità di ragionare, ad applicare intuitivamente quanto appreso a nuovi problemi e nuove soluzioni.
Per capire questo partiamo dal modo in cui si sviluppa il pensiero e la logica razionale, ovvero il processo induttivo e quello deduttivo.
Pensiero induttivo
Col pensiero induttivo il programmatore parte da un insieme di informazioni in suo possesso (ad esempio il testo di un esercizio, o un insieme di richieste del committente, o un funzionamento spiegato per esempi o altro ancora) e, tramite un processo di ragionamento, arriva alla produzione di leggi o regole generali. Queste regole generali sono necessarie perchè un sistema automatico ovvero un computer funziona tramite istruzioni che funzionano appunto tramite regole generali.

Facciamo un esempio. Ci viene richiesto di scrivere un programma che calcola in automatico una approssimazione di da un numero n (inserito dall’utente), secondo la seguente espressione (detto prodotto di Wallis[1]):
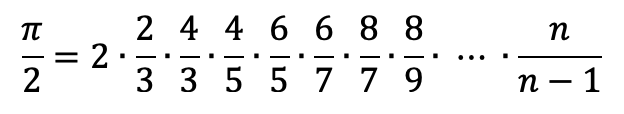
E’ evidente che non è possibile scrivere un programma dove scriviamo tutti i moltiplicandi di questa espressione. Occorre prima individuare una regola generale che rappresenta l’algoritmo da sviluppare.
E’ qui che si sviluppa il ragionamento induttivo. Possiamo osservare che la precedente formula è così scomponibile in tante coppie:
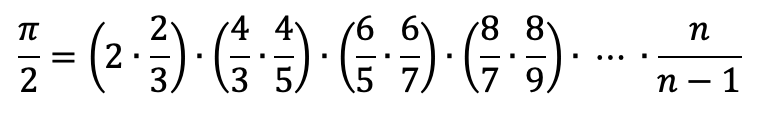
Come si vede ogni coppia ha questa struttura:
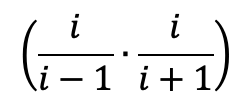
che è immediatamente verificabile con l’esempio per i = 2,4,6,8,…
Quindi il prodotto deve essere una produttoria[2] dove cambia l’indice i.
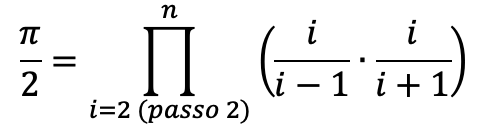
Ecco: questo è il processo di generalizzazione: a partire da una espressione si arriva ad una regola generale tramite un processo induttivo.
Quando si sviluppa il software è necessario sempre creare un modello generale che rappresenta il problema da risolvere. E’ necessario inoltre che il modello sia valido qualsiasi sia l’input del problema. In questo caso specifico questa regola funziona qualsiasi sia n (si lascia per esercizio fare qualche test).
Proviamo un altro problema. Si scriva un programma che dati due numeri a e b, ne calcoli il minimo comune multiplo. Come noto mcm è il più piccolo numero che è multiplo di a e b. Ad esempio:
| a | b | mcm |
| 10 | 15 | 30 |
| 24 | 36 | 72 |
| 20 | 10 | 20 |
| 13 | 17 | 221 |
Si ma qual è la regola generale? Una generalizzazione potrebbe essere quella di prendere i multipli del numero più grande fino a quando non se ne trova uno che è multiplo del più piccolo. Ma questo modello può essere semplice in alcuni casi (24 e 36) ma molto oneroso in altri (13 e 17) col risultato che in generale un algoritmo di calcolo di questo tipo è abbastanza inefficiente.
Un modello più efficace si basa sull’osservazione di una prima correlazione: alcune coppie di numeri come (24,36) hanno “qualcosa” in comune che invece (13,17) non ne hanno: sono i divisori primi.
| 24 | 36 | 72 | |||||
| 3 | 3 | 3 | |||||
| 2 | 3 | 3 | |||||
| 2 | 2 | 2 | |||||
| 2 | 2 | 2 | |||||
| 2 | |||||||
| 13 | 17 | 221 | |||
| 13 | 17 | 17 | |||
| 13 | |||||
Provando più casi possiamo trarre sempre per correlazione le seguenti ipotesi:
– mcm ha tutti i fattori primi NON comuni tra a e b (cioè è multiplo dei fattori primi solo di a o solo di b);
– mcm ha tutti i fattori primi COMUNI tra a e b (cioè è multiplo di tutti i fattori primi presenti sia in a che b);
– mcm NON ha fattori primi non presenti in a o b;
Da qui discende la regola generale: mcm è il prodotto di tutti i fattori primi non comuni di a e b, e di quelli comuni tra a e b, e non contiene alcun altro fattore.
Andiamo quindi a verificare le nostre ipotesi in altri casi.
1) 15 e 18 hanno rispettivamente [5,3] e [3,3,2] come fattori primi. Quelli comuni sono [3] e quelli non comuni sono [5] e [3,2]. Ci dobbiamo quindi aspettare che l’mcm sia il prodotto di [5,3,3,2] ovvero 90.
2) 14 e 20 hanno rispettivamente [7,2] e [5,2,2] come fattori primi. Quelli comuni sono [2] e quelli non comuni sono [7] e [5,2]. Mcm è quindi dato dal prodotto di [2,7,5,2] ovvero 140.
3) 36 e 48 hanno rispettivamente [3,3,2,2] e [3,2,2,2,2]. Comuni [3,2,2] e non comuni [3] e [2,2]. Il risultato sarà quindi [3,2,2,3,2,2] cioè 144.
Ancora una volta si è individuata una generalizzazione tramite processo induttivo, ovvero da un insieme di casi particolari ad una regola generale. La risoluzione dei due problemi è comunque originale e creativa, e non frutto della medesima procedura “meccanica”.
Vediamo però che c’è stato un procedimento comune:
1) Si cerca di individuare delle proprietà non immediatamente enunciate dal problema iniziale: si chiamano “ipotesi aggiuntive” e definiscono un “perimetro” di conoscenza che tiene conto anche di casi particolari (esempio mcm di due numeri primi tra loro).
2) SI cerca di fare delle ipotesi sulle correlazioni tra gli esempi a disposizione (nella formula di Wallis si nota una correlazione tra coppie di prodotti, nell’mcm le correlazioni tra fattori).
3) A questo punto si fanno delle ipotesi generali che vanno verificate con degli esempi.
Può anche accadere che alcune ipotesi induttive siano vere ma solo per un opportuno sottoinsieme dei dati a disposizione, ma non sempre ed quindi essere globalmente errate. Per capirlo leggiamo la breve storia triste del tacchino induttivista[3]:
Il tacchino osservava che nella fattoria in cui viveva gli veniva dato cibo ogni mattina ed ogni sera. Ma siccome lui conosceva il metodo induttivo, non trasse immediatamente conclusioni. Osservò che il cibo gli veniva dato anche se pioveva o c’era il sole, che veniva servito anche la domenica e nei giorni di festa, che facesse freddo o caldo. Annotava ogni circostanza collegata all’erogazione di cibo e invariabilmente osservava che il cibo veniva fornito sempre e comunque. Alla fine fu soddisfatto di ogni esperienza fatta ed arrivo alla generalizzazione che “il cibo viene sempre dato mattina e sera”.
Solo che il giorno dopo era la vigilia di Natale. ;-(
Da questa storiella dobbiamo imparare quindi che ogni nostra generalizzazione non vale “sempre” ma soltanto ” fino a prova contraria”.
Pensiero deduttivo e problem solving
Ottenuta la generalizzazione del problema, ovvero un modello, si passa alla fase successiva: realizzare un programma che traduce il modello in codice.
In questo caso entra in gioco il processo deduttivo: a partire da un modello si procede per passi allo sviluppo del programma finale:
1) Derivare dal modello generale l’algoritmo;
2) Implementare l’algoritmo in un programma codificato;
3) Verificare il programma con gli input.
4) Se ci sono errori, correggere il programma.

Il metodo deduttivo si basa sul sillogismo che possiamo spiegare con questo esempio:
- tutti gli studenti che studiano prendono la sufficienza
- lo studente Mario studia
- Quindi Mario prende la sufficienza
Vediamo cosa significa concretamente.
Nell’esempio del prodotto di Wallis eravamo giunti a questa conclusione:
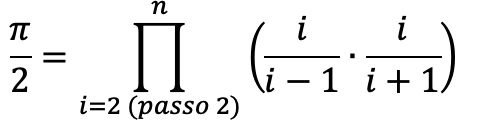
Ovvero:
- il prodotto finale è un prodotto di espressioni che dipendono da un valore i
- i va da 2 a n con passo 2 (2,4,6,8,…)
- Quindi per ogni i calcoliamo l’espressione e la moltiplichiamo per il prodotto parziale.
Da questo deduciamo l’algoritmo da sviluppare: siccome ogni prodotto dipende solo da i, lo si calcola in un ciclo e poi si esegue questo ciclo n volte.
A questo punto si passa all’applicazione tecnica dell’algoritmo, che dipende dal linguaggio di codifica e dai particolari costrutti sintattici del linguaggio.
In questo caso una soluzione in C++ sarà (si omettono header e direttive):
int main() {
double i, n, pi=1;
cout << "Inserisci valore n:";
cin >> n;
for (i = 2; i<=n; i+=2) {
pi = pi * i / (i-1) * i / (i+1);
}
pi = 2 * pi;
cout << "Il valore di pi con approssimazione " << n << " è: " << pi << endl;
return 0;
}Il programma viene poi eseguito e risolve la problematica che ha generato quel modello. Se il modello è valido, anche il programma è valido. La programmazione è un processo deduttivo, che a partire da un modello deduce un programma che è derivato dal modello stesso. La sua trasposizione in uno specifico linguaggio è una attività tecnica. Inoltre ogni linguaggio per sua natura privilegia o penalizza alcuni o altri aspetti della programmazione. Per questa ragione saper programmare significa non dipendere da uno specifico linguaggio coi suoi limiti e peculiarità, ma padroneggiare diversi linguaggi in modo da non dipendere da specificità tecniche.
Vediamo un altro esempio, quello del mcm. Come sappiamo questo è dato da:
– fattori primi comuni;
– fattori primi non comuni.
Una soluzione intuitiva è quella di calcolare i fattori primi di ciascun numero e fare tre liste, quella di quelli comuni, quelle dei non comuni e infine moltiplicare tutti i fattori insieme. Questo approccio, per quanto funzionante, è piuttosto “brutale” in quanto produce un algoritmo inefficiente che richiede molto calcolo (bisogna infatti calcolare i fattori primi di ciascun numero) e molta memoria (per memorizzarli da qualche parte).
Possiamo usare un altro approccio, che si fonda sui seguenti sillogismi:
– un mcm è il prodotto dei fattori primi comuni di a e b;
– un mcm è il prodotto dei fattori primi non comuni;
Quindi:
– ogni numero che è fattore di a e b è moltiplicando di mcm, ogni numero che è fattore solo di a o di b è moltiplicando di mcm.
Da queste considerazioni, possiamo ricostruire mcm procedendo in modo incrementale:
– si parte dal più piccolo fattore (2, visto che 1 è fattore di qualsiasi numero);
– si verifica se è divisore di entrambi i numeri, o di solo a o b.
– se lo è diventa moltiplicando di mcm e quindi si divide per il fattore a e b oppure a oppure b, e si ripete il procedimento;
– se non lo è si incrementa il fattore di 1, e si ripete il procedimento.
– si esce dal ciclo quando a e b valgono 1.
Qui il codice C++:
int main() {
int a,b;
cout << "Inserisci a: ";
cin >> a;
cout << "Inserisci b: ";
cin >> b;
int mcm = 1;
int factor = 2;
while (a > 1 || b > 1) {
if (a%factor == 0 && b%factor == 0) {
mcm = mcm * factor;
a = a / factor;
b = b / factor;
} else if (a%factor == 0) {
mcm = mcm * factor;
a = a / factor;
} else if (b%factor == 0) {
mcm = mcm * factor;
b = b / factor;
} else {
factor++;
}
}
cout << "Il mcm è: " << mcm << endl;
return 0;
}Per esercizio, testare con diverse coppie di valori per verificare la correttezza dell’algoritmo.
Questa soluzione è molto efficiente, usa un solo ciclo, non memorizza nulla.
Questo tipo di approccio si chiama “euristico”: consiste nel procedere per tentativi per trovare la soluzione. Si fa una ipotesi e la si verifica: se valida la si adotta, altrimenti si procede verso altra direzione. Grazie all’euristica possono essere individuati elementi utili alla risoluzione del problema che possono semplificare la realizzazione dell’algoritmo. In alcune tipologie di problemi molto complessi l’euristica non porta a soluzioni “formalmente” corrette, ma consente con poco sforzo di ottenere una approssimazione del risultato voluto.
Altri approcci
Approccio partitivo
Consiste nel dividere un problema in parti più semplici, risolverle separatamente ed infine unirle insieme.
Questo approccio è usato in tutti i progetti di media e grande complessità. La suddivisione del problema può essere per funzione: ad esempio un programma che carica da un database informazioni, le elabora e poi le presenta all’utente può essere visto come 3 programmi distinti, uno che carica le informazioni, uno che le elabora ed infine un programma che visualizza i dati elaborati. Un altro esempio è un programma che si occupa di eseguire un ordinamento di una grande lista di dati complessi: esso può essere scomposto in due probemi distinti: uno che si occupa dell’ordinamento di un insieme generico, ed un altro che si occupa di confrontare solo due elementi per capire in che ordine vanno messi.
In questa categoria di risoluzioni rientra anche il “divide et impera”, dove i sottoproblemi sono tutti dello stesso tipo, e cambiano solo i parametri (che sono via via semplificati). In questo caso assume molta importanza anche la parte di unione. Lo vedremo negli algoritmi ricorsivi.
Approccio per modelli
Per molte tipologie di problemi esistono dei “modelli di algoritmi”.
Come sappiamo un algoritmo non risolve uno specifico input, ma risolve un problema generale. Un modello è l’estensione di un algoritmo: non risolve uno specifico problema, ma da una soluzione per molti problemi simili. Occorre quindi adattarlo ad uno specifico problema.
Ad esempio quando molti componenti software devono comunicare tra loro in una rete interna, magari senza neppure conoscersi, può essere utile creare un nuovo componente conosciuto da tutti che fa da mediatore. Questo tipo di problema viene risolto da un modello che si chiama proprio “Mediatore”.
Problemi non risolvibili “velocemente”
Infine, va ricordato che non tutti i problemi sono risolvibili “velocemente”. Alcuni esempi di algoritmi che a seconda dell’input possono avere una complessità notevole ed in questi casi si procede per tentativi, ovvero tramite forza bruta. Alcuni esempi li abbiamo visti come il calcolo dei numeri primi o il calcolo dei divisori di un numero.
[1] Tanto più grande è n, tanto migliore è l’approssimazione di (https://it.wikipedia.org/wiki/Prodotto_di_Wallis)
[2] In matematica la produttoria è una operazione che sintetizza una moltiplicazione di fattori, che usa il simbolo ∏ seguito da due indici: la variabile con valore iniziale e il valore finale. Qui un riferimento: https://it.wikipedia.org/wiki/Produttoria
[3] Si tratta di una celebre metafora del Karl Popper, intesa a spiegare i limiti del processo induttivo.
