Science Technology and Technique

To fully understand the relationship between science, technology and technique, we must first define these terms clearly and unambiguously.

To understand this we will start with ancient Greece and the early philosophers, because it was from them that Western civilization and thought developed: it was at that time that the first disciplines of study, such as mathematics, physics, and philosophy, were born.

The first great thinkers (Thales, Pythagoras, Democritus) were at once philosophers, mathematicians, scientists, and inventors. To indicate their work they often used two words that at least initially were shades of the same concept: epistéme (“knowledge, truth”) and téchne (“art, expertise”). The thinker was in fact a kind of all-rounder, concerned with all sciences, both thought and practical.

It is only since the philosopher Aristotle that the distinction becomes sharper. Epistéme becomes abstract knowledge, a general knowledge of the world without practical repercussions, while téchne becomes the “art, craft,” that is, concrete knowledge, which did not need abstraction.

The concept of science stems precisely from Aristotle’s definition: that is, it is that discipline, or set of disciplines, which are concerned with knowing and understanding reality through some level of abstraction, that is, through the creation of “models,” which become general concepts, with their own consistency and coherence, independent of their real counterpart.

Thus in science we can start from a wheel and abstract the concept of “circle,” and so on from real experience we can define the other geometric figures, such as triangle, rectangle, etc. These entities although coming from reality are still abstract ideas, that is, not dependent on a specific real experience: the circle is a circle and no longer depends on the concept of a wheel, or disk, or a ring (and so for the other figures). Moreover, these abstract ideas can be related to each other, and complex patterns can also be created, which no longer depend directly on reality, but which serve us to create our own more complete idea of what is “behind” reality, interconnected with it but still the result of deductions and reasoning, called theories.[1]

What we call technique, on the other hand, is the set of activities of constructing means and tools to perform certain functions. Technique is the result of empirical practice, invention and may also involve theoretical knowledge but always linked to a practical end. In technique the end is practical, that is, making artifacts.

The ancient Egyptians were aware of Pythagoras’ theorem (in a right triangle, the square built on the hypotenuse is the sum of the squares built on the cathexes) and Euclid’s postulate (two parallel lines meet at infinity), and they made extensive use of it to recalculate the division of land when the Nile flooded. The pyramids were always built on the basis of the same mathematics, which we can consider part of their technical background of knowledge.

Instead, the mathematics of the ancient Greeks was based on a set of fundamental abstract axioms from which all the fundamental theorems and laws, such as Pythagoras’ theorem and Euclid’s theorem, could be deduced by logic. The knowledge of the Greeks started from experience but was abstract and general.

Yet in both mathematics there is the Pythagorean theorem. But in one case – that of the Egyptians – it is part of an applied reality, while in the other – that of the Greeks – it becomes part of a general system namely Euclidean geometry.

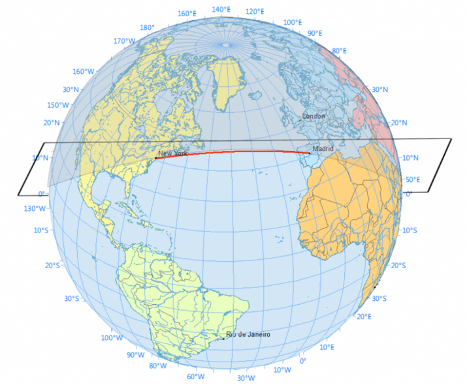
It is not a detail. Euclidean geometry is an abstract system that is not strictly valid in practice. It may be fine for making the Pyramid of Cheops and for measurements of land up to a few kilometers, but it is certainly not fine when the magnitudes are thousands of kilometers. If you look at a planisphere the “meridians” are not really parallel to each other but converge at the North Pole. This is why intercontinental air travel (e.g., from Milan to New York) involves a curved trajectory that takes this problem into account. The mathematics of the Egyptians would never have come to understand that Euclidean geometry is only applicable to part of reality. That of the Greeks got there.

From this we understand a few things.

• That technology arises from practical needs and thus comes before science. Man has known how to create fire for 400,000 years, and has known the wheel for at least 10,000. The ancient Egyptians knew geometry long before the Greeks, and it enabled them to build the Pyramids;
• science, however, is capable of solving problems that cannot be solved by technique alone: with a general understanding, not dependent on a specific practical application, we have been able to go beyond the limits of experimental practice and solve otherwise unsolvable problems: the airplane, atomic energy, space exploration.

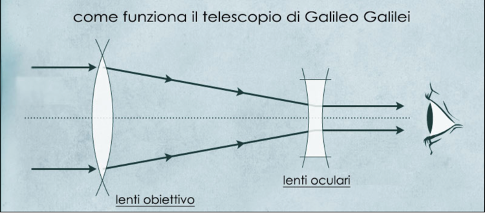
To sum up, science and technology thus differ in method (practical or abstract) and goals (theories or artifacts), but both have knowledge and knowledge as their object in some way. A great many scientists were and are also technically proficient in making and handling tools useful for scientific and experimental research. For example, Galileo built his own telescope, and with that he made his astronomical discoveries. To give another example, researchers at CERN (in Geneva) study theories of matter and particles with a particle accelerator (a circular underground structure tens of kilometers long).

Let us now turn to technology.

The ancient Romans were in many respects technically advanced (think roads, bridges, aqueducts) but they were not particularly good at creating machine models independent of their practical application. When they learned from the Greeks the use of catapults they began to reproduce them from those captured and not from the ballistic theories with which they were designed. In a few decades, making copies of copies, and then copying their own copies again, because they did not quite understand how catapults worked, over time they introduced such flaws as to make them less and less effective until they became completely useless.

So not just great technical skill, but there is a need for a discipline created abstract models of the artifacts and empirical practice, so that an “idea” of the product is saved and passed on.

Technology is just that: it is a theory that studies, from technique and science, a set of models that can be useful for practical manufacturing processes. It is thus both a “theory of technique” and an “applied science,” and it bridges the gap present between the two disciplines. In fact, technology exploits the models of science to evolve models of artifacts and thus also the technique of making them. One example is the mechanical industry: the great discoveries about thermodynamics gave impetus to the making of engines, trains, and automobiles.

But technology is a fundamental discipline regardless of the existence of science making new discoveries. For it also goes on to generalize practical experience, experimental improvements, without these being lost as happened with the Greek catapults. Galileo’s telescope was a result of technology, the technology after Galileo on the other hand exploits the science of optics and technical advances together to model more and more powerful telescopes that will then be made by specific technique from technology.

Science therefore studies and makes models of reality, and tests them experimentally.

Technique studies the ability to build increasingly useful objects.

Technology is an applied science that studies how to build objects.

What about computer science?

Computer science is first and foremost a science: a science that studies information and automatic information processing. It therefore partly overlaps with mathematics (which also studies information). It is because of this science that we now have models such as algorithms, data structures, databases, and artificial intelligence. But computer science also tells us how computers should be made, that is, the tools that actually process information automatically, and is therefore also a technology.

What, on the other hand, is computer science not? It is not a technique in the strict sense, so it is not based on practical experience, although every computer scientist with experience also acquires a strong practical component.