Introduzione allo sviluppo del software
Lo sviluppo del software consiste nella creazione di programmi ed applicazioni per sistemi informatici attraverso una attività che prevede un insieme di fasi, fa uso di strumenti e competenze tecnologiche e progettuali (come i linguaggi di programmazione, la conoscenza degli algoritmi e delle strutture dati, ecc.), ed è supportata da un insieme di strumenti software che consentono di automatizzare alcune parti del procedimento.
Lo sviluppo di software è una attività creativa, e quindi non esiste una procedura meccanica per risolvere qualunque tipo di problema. Ogni problema è diverso, con un proprio modello concettuale e quindi algoritmi specifici per la sua risoluzione.
La programmazione inoltre non è la semplice conoscenza di un linguaggio di programmazione e non si riduce ad una semplice attività di coding. E’ invece fondamentale capire che lo sviluppo del software inizia molto prima, ed attraversa un insieme di fasi che vanno oltre il coding stesso, ed arrivano fino al definitivo rilascio del software finito.
Possiamo schematizzare queste fasi nel seguente modo:

Tra queste rivestono particolare importanza le prime due fasi, che determinano di fatto tutte le scelte progettuali e tecnologiche delle ultime fasi.
Definizione del modello: il pensiero induttivo
Per progettare una applicazione occorre sviluppare un modello generale che rappresenta l'”universo” del problema da risolvere. Il programmatore parte dai requisiti richiesti e da un insieme di informazioni che raccoglie sulla realtà di riferimento di questi requisiti e, tramite un processo di ragionamento logico, detto induzione, arriva alla produzione di leggi o regole generali.
L’induzione è quel procedimento logico che appunto parte dal particolare ed arrivare ad avere una comprensione generale di un determinato insieme di esperienze e fenomeni analizzati.
E’ sempre necessario arrivare a regole generali: un algoritmo per computer infatti non si basa su casi particolari, ma deve funzionare per qualsiasi insieme di dati che gli viene sottoposto per quello specifico problema. E’ quindi necessario avere una conoscenza ampia e completa del contesto in cui sviluppare una soluzione ad un problema.
Obiettivo del processo induttivo è quindi quello di di analizzare un determinato problema da risolvere e a partire dalla realtà di riferimento, costituita da un insieme di esperienze, esempi, dati di riferimento, ecc. ed arrivare a costruire un modello generale che vada bene sia per gli esempi ricevuti sia per qualsiasi tipo di dato compatibile con quel problema.
Per capire questo concetto partiamo da un problema concreto, dobbiamo trovare un modello generale per calcolare la circonferenza del cerchio a partire dal diametro. Certo noi sappiamo già come si calcola ma ipotizziamo di volerlo scoprire per conto nostro. Ci serve una regola generale che ci permetta di calcolare la circonferenza dato il raggio, in modo tale da non doverlo fare ogni volta a mano.
Per risolvere questo problema in modo induttivo dobbiamo quindi partire da un un insieme di circonferenze che disegneremo in un foglio (ad esempio con un goniometro) e misurare per ciascuna di esse la relativa circonferenza ed il diametro e vedere se c’è qualche correlazione. Qui un esempio di valori misurati concretamente:
| Diametro (cm) | Circonferenza (cm) |
| 5 | 15,71 |
| 9 | 4,25 |
| 6 | 18,85 |
| 12 | 37,70 |
E così via. Notiamo che esiste una correlazione tra diametro e circonferenza (al netto di errori di misura) che non cambia mai qualsiasi sia il raggio ed è approssimabile ad un valore che è circa 3,1415… . Non solo ma possiamo verificarlo col processo inverso, disegnando una circonferenza, da cui calcoliamo il diametro e poi confrontandolo con la nostra ipotesi.
Possiamo sintetizzare con la grafica seguente il procedimento che abbiamo appena seguito:

Ora proviamo a fare un altro esempio. Vogliamo usare il procedimento induttivo non per trovare una formula generale, ma per semplificarne una esistente, sempre legata al mondo del pi greco, e più precisamente dal prodotto di Wallis, un procedimento algebrico che consente di calcolare la misura di π tramite un prodotto di frazioni: [1]
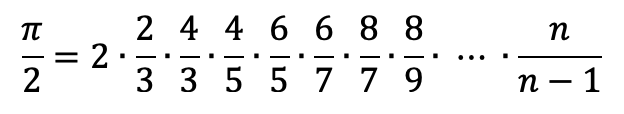
maggiore è il valore di n, più precisa l’approssimazione di π.
Ci viene quindi richiesto di scrivere un programma che dato n ci calcoli una approssimazione di pi greco.
La soluzione è quella di calcolare tutti i moltiplicandi di questa espressione e poi di moltiplicarli tra loro. Ma per farlo è necessario trovare una regola che consenta di eseguire questo procedimento in modo iterativo, sulla base di una variabile i che viene incrementata fino a raggiungere n.
Se analizziamo il prodotto possiamo infatti osservare che esso è scomponibile (mediante la proprietà associativa della moltiplicazione) nel seguente modo:
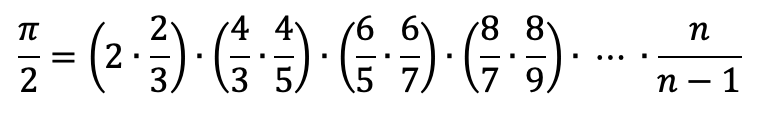
Come si vede ogni coppia ha questa struttura:
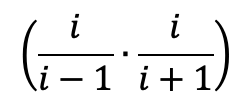
che è immediatamente verificabile con l’esempio per i = 2,4,6,8,…
Quindi il prodotto si può semplificare con una espressione produttoria[2], dove ogni elemento dipende da un indice i che va da 2 a n con passo 2 (quindi 2,4,6,8, …).
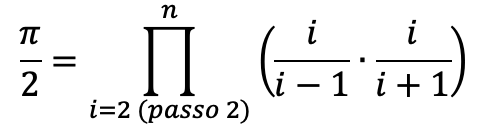
Il procedimento induttivo quindi non solo serve a trovare una regola in base a degli esperimenti, ma ci consente di generalizzare regole più complicate in regole più semplici.
Proviamo a vedere un terzo esempio. Ci è richiesto di scrivere un programma che dati due numeri a e b, ne calcoli il minimo comune multiplo. Come noto mcm è il più piccolo numero che è multiplo sia di a che di b. Ad esempio:
| a | b | mcm |
| 10 | 15 | 30 |
| 24 | 36 | 72 |
| 20 | 10 | 20 |
| 13 | 17 | 221 |
Una soluzione al problema consiste nel procedere per tentativi con i multipli del numero più grande fino a quando non se ne trova uno che è multiplo anche del più piccolo. Questo algoritmo è corretto, può essere molto efficiente in alcuni casi (per 24 e 36 per esempio ci basta 1 tentativo) ma molto inefficiente in altri (13 e 17 hanno bisogno di ben 13 tentativi). Se facciamo molte prove ci accorgiamo che il numero medio di tentativi può essere molto alto.
Intuiamo che se riuscissimo a capire perché, potremmo semplificarlo e di molto.
Proviamo quindi ad osservare quando i tentativi sono pochi e quando invece sono molti. Ad esempio 24 e 36 richiedono 2 tentativi, mentre 13 e 17 ne richiedono 13. Evidentemente c’è qualcosa in comune tra i primi due. Proviamo quindi a scomporre 24, 36 e 72 in fattori primi:
| 24 | 36 | 72 | |
| 3 | 3 | 3 | |
| 2 | 3 | 3 | |
| 2 | 2 | 2 | |
| 2 | 2 | 2 | |
| 2 | |||
Ora vediamo 13, 17 e 221:
| 13 | 17 | 221 | |
| 13 | 17 | 13 | |
| 3 | 17 | ||
Come si può vedere:
– mcm ha tutti i fattori primi NON comuni tra a e b;
– mcm ha tutti i fattori primi COMUNI tra a e b (cioè è multiplo di tutti i fattori primi presenti sia in a che b) presi però una volta sola;
– mcm NON ha fattori primi non presenti in a o b;
Andiamo quindi a verificare le nostre ipotesi in altri casi.
1) 15 e 18 hanno rispettivamente [5,3] e [3,3,2] come fattori primi. Quelli comuni sono [3] e quelli non comuni sono [5] e [3,2]. Ci dobbiamo quindi aspettare che l’mcm sia il prodotto di [5,3,3,2] ovvero 90.
2) 14 e 20 hanno rispettivamente [7,2] e [5,2,2] come fattori primi. Quelli comuni sono [2] e quelli non comuni sono [7] e [5,2]. Mcm è quindi dato dal prodotto di [2,7,5,2] ovvero 140.
3) 36 e 48 hanno rispettivamente [3,3,2,2] e [3,2,2,2,2]. Comuni [3,2,2] e non comuni [3] e [2,2]. Il risultato sarà quindi [3,2,2,3,2,2] cioè 144.
Abbiamo quindi trovato la regola generale: anziché moltiplicare uno dei due numeri, li scomponiamo in fattori primi e poi calcoliamo il loro mcm. Con questo metodo ci saranno situazioni dove si svolgono più operazioni che con l’altro metodo, ma in generale è più efficiente soprattutto per numeri molto grandi.
Verificarlo per esercizio.
Conclusioni
Da questa procedura possiamo quindi capire in cosa consiste l’analisi del problema tramite induzione.
Questo procedimento si può quindi descrivere nel seguente modo:
1) Si cerca di individuare delle proprietà non immediatamente enunciate dal problema iniziale: si chiamano “ipotesi aggiuntive” ed allargano le nostre conoscenze sul problema partendo dall’osservazione di esempi concreti di dati da elaborare.
2) Questa conoscenza aggiuntiva ci permette di fare delle ipotesi sulle correlazioni tra gli esempi a disposizione (nella formula di Wallis si nota una correlazione tra coppie di prodotti, nell’mcm le correlazioni tra fattori).
3) A questo punto si propone una regola generale, che va nuovamente verificata con i dati iniziali ma anche con nuovi dati per validarla.
Il terzo punto è molto importante, perché può anche accadere che esistano delle correlazioni tra i dati presi ad esempio, ma che non sono valide in generale perché i dati di esempio sono in qualche modo viziati da qualche problema di correlazione tra loro.
Per capirlo leggiamo la breve storia triste del tacchino induttivista[3]:
Il tacchino osservava che nella fattoria in cui viveva gli veniva dato cibo ogni mattina ed ogni sera. Ma siccome lui conosceva il metodo induttivo, non trasse immediatamente conclusioni. Osservò che il cibo gli veniva dato anche se pioveva o c’era il sole, che veniva servito anche la domenica e nei giorni di festa, che facesse freddo o caldo. Annotava ogni circostanza collegata all’erogazione di cibo e invariabilmente osservava che il cibo veniva fornito sempre e comunque, ogni mattina ed ogni sera. Alla fine fu soddisfatto di ogni esperienza fatta ed arrivo alla generalizzazione che “il cibo viene sempre dato mattina e sera”.
Una generalizzazione che si rivelo tuttavia errata. Infatti il giorno dopo era la vigilia di Natale.
Da questa storiella dobbiamo imparare quindi che ogni nostra generalizzazione non vale “sempre” ma soltanto ” fino a prova contraria” e che il metodo induttivo è valido ma non infallibile.
Quando si sviluppa il software è necessario creare un modello generale che rappresenta il problema da risolvere. E’ necessario inoltre che il modello sia valido qualsiasi sia l’input del problema e quindi dobbiamo verificarlo coi dati a nostra disposizione, ed anche con nuovi dati, per capire se effettivamente la soluzione individuata ha senso.
Pensiero deduttivo
Ottenuta la generalizzazione del problema, ovvero un modello, si passa alla fase successiva: realizzare un programma che traduce il modello in codice.
In questo caso entra in gioco il processo deduttivo: a partire da un modello si procede per passi allo sviluppo del programma finale:
1) Derivare dal modello generale l’algoritmo;
2) Implementare l’algoritmo in un programma codificato;
3) Verificare il programma con gli input.
4) Se ci sono errori, correggere il programma.

Il metodo deduttivo è il procedimento di base che serve a mettere insieme tutto quell’insieme di metodi algoritmici e paradigmi di programmazione. Esso si basa su un insieme di metodi, come il sillogismo, la logica proposizionale e la logica dei predicati.
Il sillogismo si basa su una coppia di proposizioni considerate vere ed una terza proposizione conseguente ad esse:
- tutti gli studenti che studiano prendono la sufficienza
- lo studente Mario studia
- Quindi Mario prende la sufficienza
Il sillogismo è un procedimento che consiste nel ricavare nuova informazione non a partire dai dati concreti, ma da precedenti affermazioni generali, tramite un collegamento tra queste.
La logica proposizionale si fonda invece sulla composizione di enunciati che possono essere veri o falsi, tramite connettori: negazione (NOT), congiunzione (AND), disgiunzione (OR), implicazione, condizione necessaria e sufficiente (se e solo se). Essa produce per ciascun gruppo di affermazioni composte una tabella di verità, che calcola se una affermazione è composta è vera/falsa sulla base delle singole affermazioni che la compongono.
La logica dei predicati è un metodo logico che formalizza una proprietà di un oggetto o una relazione tra oggetti:
- x è maggiore di 0;
- se z < y allora
- per ogni x divisibile per 2 allora esiste un y tale che y = x / 2
Essa prevede la definizione di variabili (x, y, ecc.), non definite esplicitamente ma da regole, costanti (valori immutabili) e funzioni (operazioni di calcolo) e la loro combinazione per definire regole che possono essere vere o false. Sono poi previsti quantificatori come ∀ (“per tutti gli elementi”) o ∃ (“esiste almeno un elemento”) per variabili di un insieme.
In pratica la logica dei predicati permette di definire regole logiche introducendo la quantificazione, gli insiemi, ed il concetti di trasformazione, appartenenza ed esistenza.
Questi procedimenti insieme consentono di sviluppare algoritmi, che mettono insieme sia le nostre conoscenze algoritmiche e di programmazione (espressioni, condizioni, cicli, variabili, strutture dati, ecc.) con quelle del problema già modellizzato (la formula semplificata di Wallis, il calcolo dei fattori primi, ecc.).
Vediamo cosa significa concretamente.
Nell’esempio del prodotto di Wallis eravamo giunti a questa conclusione:
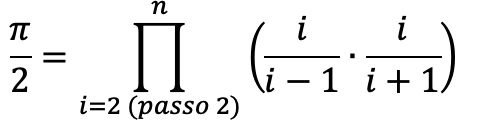
Ovvero:
- il prodotto finale è un prodotto di espressioni che dipendono da un valore i
- i va da 2 a n con passo 2 (2,4,6,8,…)
- Quindi per ogni i calcoliamo l’espressione e la moltiplichiamo per il prodotto parziale.
A questa regola associamo quanto già sappiamo dei cicli:
- un ciclo è una sequenza di operazioni di ripetute;
- un ciclo ad iterazione definita è un tipo di ciclo dove possiamo usare un indice i che va da X a Y con passo Z.
Correliamo tramite sillogismo queste due conoscenze che abbiamo:
- è possibile fare un ciclo ad iterazione definita da i=2 a n con passo 2.
Ecco il nostro algoritmo di calcolo.
A questo punto si passa all’applicazione tecnica dell’algoritmo, che dipende dal linguaggio di codifica e dai particolari costrutti sintattici del linguaggio.
In questo caso una soluzione in C++ sarà (si omettono header e direttive):
int main() {
double i, n, pi=1;
cout << "Inserisci valore n:";
cin >> n;
for (i = 2; i<=n; i+=2) {
pi = pi * (i / (i-1)) * (i / (i+1));
}
pi = 2 * pi;
cout << "Il valore di pi con approssimazione " << n << " è: " << pi << endl;
return 0;
}Il programma va poi eseguito e va verificato se effettivamente risolve la problematica che ha generato quel modello. Per farlo dobbiamo sperimentarlo con gli esempi a nostra disposizione, facendo molta attenzione a proporre al programma un set valido di esempi che copra anche situazioni particolari.
Vediamo un altro esempio, quello del mcm. Come sappiamo questo è dato da:
– fattori primi comuni;
– fattori primi non comuni.
Una soluzione intuitiva è quella di calcolare i fattori primi di ciascun numero e fare tre liste, quella di quelli comuni, quelle dei non comuni e infine moltiplicare tutti i fattori insieme. Questo approccio, per quanto funzionante, è piuttosto “brutale” in quanto produce un algoritmo inefficiente che richiede molto calcolo (bisogna infatti calcolare i fattori primi di ciascun numero) e molta memoria (per memorizzarli da qualche parte).
Possiamo usare un altro approccio che sfrutta alcuni sillogismi. Come sappiamo infatti:
– un mcm è il prodotto dei fattori primi comuni di a e b;
– un mcm è il prodotto dei fattori primi non comuni;
Ma questo vuol dire che:
- se il numero x è fattore primo di a ma non di b, allora è fattore primo anche di mcm
- se il numero x è fattore primo di b ma non di a, allora è fattore primo anche di mcm
- se il numero x è fattore primo sia di a che di b, allora è fattore primo anche di mcm
Inoltre:
- qualsiasi numero i (da 2 in avanti) è fattore primo di un numero K se K è divisibile per i. K viene poi diviso per K e si ricomincia. Se non è divisibile per i, allora i=i+1 e si ricomincia.
Da queste considerazioni, possiamo ricostruire mcm procedendo in modo incrementale:
1) si parte da i=2 e mcm=1
2) se i è divisore di a o b, allora mcm = mcm * i. Si divide a o b o entrambi per i.
3) altrimenti si incrementa i=i+1
4) se a=1 e b=1 abbiamo finito, altrimenti si torna al punto 2
Si tratta di un ciclo ad iterazione indefinita, dove la variabile sentinella è data a e b.
Qui il codice C++:
int main() {
int a,b;
cout << "Inserisci a: ";
cin >> a;
cout << "Inserisci b: ";
cin >> b;
int mcm = 1;
int factor = 2;
while (a > 1 || b > 1) {
if (a%factor == 0 && b%factor == 0) {
mcm = mcm * factor;
a = a / factor;
b = b / factor;
} else if (a%factor == 0) {
mcm = mcm * factor;
a = a / factor;
} else if (b%factor == 0) {
mcm = mcm * factor;
b = b / factor;
} else {
factor++;
}
}
cout << "Il mcm è: " << mcm << endl;
return 0;
}Per esercizio, testare con diverse coppie di valori per verificare la correttezza dell’algoritmo.
Questa soluzione è molto efficiente, usa un solo ciclo, non memorizza nulla.
Conclusioni
La programmazione è un processo deduttivo, che a partire da un modello deduce un programma che è derivato dal modello stesso.
La sua trasposizione in uno specifico linguaggio è invece una pura attività tecnica che richiede competenze specifiche ma che non ha alcun valore se dietro non c’è una conoscenza dei principi ed i fondamenti della programmazione.
In altre parole la sola conoscenza di linguaggi ci da accesso solo a dei formalismi, ma senza la capacità di utilizzare i processi induttivi e deduttivi non siamo in realtà in grado di programmare.
Inoltre ogni linguaggio per sua natura privilegia o penalizza alcuni o altri aspetti della programmazione. Per questa ragione saper programmare significa non dipendere da uno specifico linguaggio coi suoi limiti e peculiarità, ma padroneggiare diversi linguaggi in modo da non dipendere da specificità tecniche.
[1] https://it.wikipedia.org/wiki/Prodotto_di_Wallis
[2] In matematica la produttoria è una operazione che sintetizza una moltiplicazione di fattori, che usa il simbolo ∏ seguito da due indici: la variabile con valore iniziale e il valore finale. Qui un riferimento: https://it.wikipedia.org/wiki/Produttoria
[3] Si tratta di una celebre metafora del Karl Popper, intesa a spiegare i limiti del processo induttivo.
[4] Il sillogismo e la stessa logica sono frutto del pensiero del filosofo Aristotele.
