Diagrammi di flusso
Gli algoritmi
Un programma per computer è un insieme di istruzioni codificate che il computer esegue per svolgere uno o più determinati compiti. Si ricorda che un programma è memorizzato nella memoria centrale, viene eseguito dalla CPU, e funziona mediante l’elaborazione di dati ed informazioni, che riceve dal mondo esterno tramite le periferiche di INPUT, come ad esempio la tastiera il mouse, e di OUTPUT, come ad esempio il monitor.
Le istruzioni di un programma eseguono un algoritmo, cioè una sequenza di istruzioni matematiche e logiche che permettono di ottenere un risultato partendo da dei dati e delle informazioni. I programmi più complessi possono comprendere anche più algoritmi che collaborano tra loro per svolgere operazioni complesse.
Ricordiamo le 6 caratteristiche di un algoritmo:
– correttezza: deve funzionare correttamente;
– generalità: non deve dipendere da un set di dati particolare;
– finitezza: deve avere un numero finito di istruzioni per terminare;
– efficienza: non deve fare operazioni inutili;
– non ambiguità: le istruzioni non devono essere ambigue o contradditorie;
– completezza: devono essere considerati tutti i casi possibili;
Prima di poter scrivere un programma per computer è necessario quindi imparare a scrivere algoritmi, capirne le logiche di progettazione, imparare e gestire i dati e la loro elaborazione.
Per questa ragione possiamo usare i diagrammi di flusso.
Diagrammi di flusso
I diagrammi di flusso prevedono quattro simboli che indicano le quattro operazioni fondamentali di un algoritmo:
– inizio o fine;
– input o output;
– assegnazione e/o calcolo di espressioni;
– verifica di condizioni.
Tutti i simboli sono connessi tra loro da frecce direzionali.
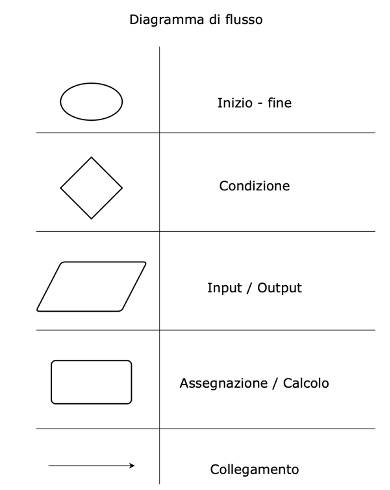
Tutti i simboli hanno un solo connettore in ingresso ed uno solo in uscita, tranne la condizione che ha due connettori in uscita.
Come vedremo, possiamo rappresentare con questi quattro simboli qualsiasi programma per computer[1].
Esempio: calcolo della somma di due numeri.
Questo programma richiede in input due numeri a e b e restituisce un risultato c pari ad a+b.
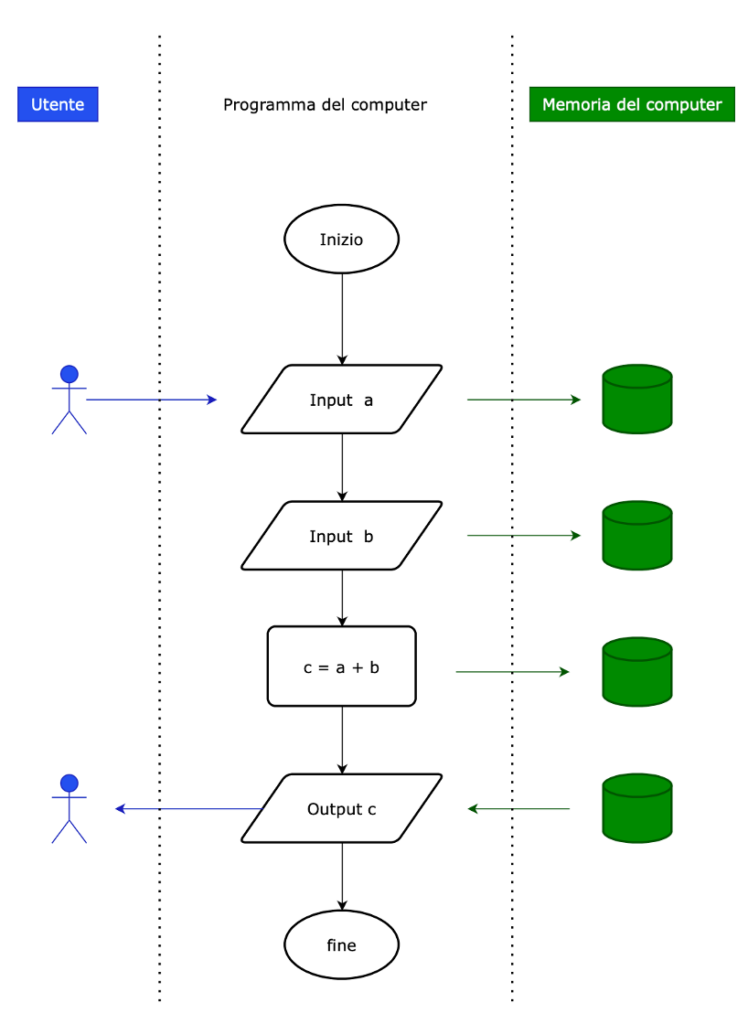
Come si vede l’utente interagisce con gli input output (parallelogramma), mentre la memoria del computer memorizza valori immessi in input (parallelogramma) oppure calcolati. Inoltre la memoria del computer contiene i valori inviati all’utente tramite output.
Per memorizzare valori introduciamo il concetto di variabile: una variabile è una area di memoria, identificata con un nome (detto identificatore, ad esempio “a” o “b”) che contiene un valore. Questo valore può cambiare anche nel corso del programma, per questo si chiama appunto “variabile”.
E’ l’utente che stabilisce il valore della variabile, quindi il programma deve funzionare senza conoscere il valore della variabile, per rispettare il principio di generalità.
Esempio: pari o dispari
Questo programma richiede un numero a, e dice se è pari o dispari.
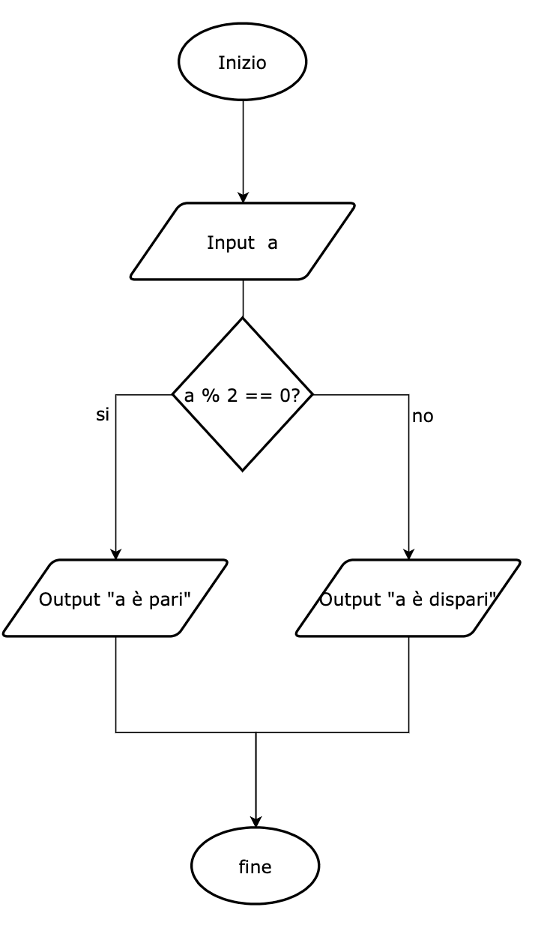
Come si vede, dopo l’input, il programma effettua una verifica: “a%2==0”. Il simbolo “%” indica il resto della divisione, mentre “==” indica un confronto di uguaglianza. Questa espressione è VERA se a % 2 è uguale a 0, altrimenti è FALSA. Ad esempio, con a=4 l’espressione è vera: a%2 è infatti uguale a 0. Invece con a=5, l’espressione è FALSA.
Come si vede, vengono rispettate tutte le caratteristiche di un algoritmo:
– correttezza: qualsiasi sia il numero inserito, il risultato è corretto;
– generalità: l’algoritmo non dipende da un particolare input;
– finitezza: l’algoritmo in qualsiasi caso termina in un numero finito di istruzioni;
– efficienza: l’algoritmo non si perde in inutili calcoli.
– non ambiguità: non ci sono contraddizioni;
– completezza: sono considerati tutti i casi possibili;
Esempio: conta fino a n
In questo programma chiediamo all’utente un numero n, ma stavolta stampiamo tutti i valori da 1 a n.
Stavolta non basta calcolare una espressione, ma dobbiamo usare un contatore e soprattutto un ciclo.
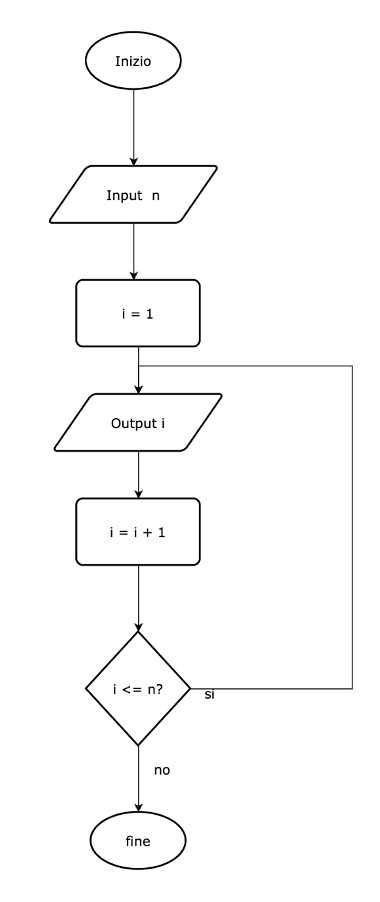
Vediamo i passaggi:
1) Viene richiesto n
2) La variabile i viene inizializzata ad 1.
3) La variabile i viene stampata.
4) i viene incrementata di 1.
5) Se i è ancora minore o uguale a n, si torna al punto 3, altrimenti si va al punto 6
6) fine.
Ad esempio per n= 5 avremo:
i=1 -> si torna al punto 3 perchè i<=5
i=2 -> si torna al punto 3 perchè i<=5
i=3 -> si torna al punto 3 perchè i<=5
i=4 -> si torna al punto 3 perchè i<=5
i=5 -> si torna al punto 3 perchè i<=5
i=6 -> si va al punto 7, perchè i > 5
I punti 3-4-5 vengono effettuati molte volte: per la precisione n volte.
Ogni ripetizione si chiama ciclo.
Il numero di cicli è determinato da n.
Con n=10 avremo 10 cicli, con n=1000 avremo 1000 cicli e così via. E’ possibile anche avere milioni di cicli, scegliendo n molto grande.
Come possiamo vedere anche un algoritmo semplice, con solo 7 passaggi come in questo diagramma di flusso, può portare all’esecuzione, grazie ai cicli, di migliaia o milioni di cicli.
Tuttavia l’algoritmo mantiene sempre le sue quattro caratteristiche:
– correttezza: qualsiasi sia il numero inserito, il risultato è corretto;
– generalità: l’algoritmo non dipende da un particolare input;
– finitezza: l’algoritmo in qualsiasi caso termina in un numero finito di istruzioni;
– efficienza: l’algoritmo non si perde in inutili calcoli.
– non ambiguità: non ci sono contraddizioni;
– completezza: sono considerati tutti i casi possibili;
[1] Come vedremo questa affermazione è alla base del teorema fondamentale della programmazione, il teorema di Bohm-Jacopini.
