Alberi in C++
Alberi
Gli alberi, in informatica, sono una delle tipologie fondamentali di struttura dati complessa, insieme agli array, alle liste e ai grafi. Un albero è una generalizzazione del concetto di lista concatenata. Se infatti nella lista concatenata ogni nodo prevede un arco che punta al nodo successivo, nell’albero invece sono previsti per ogni nodo più archi che puntano ad altri nodi. Qui un esempio di albero dove sono previsti due puntatori per ogni nodo:
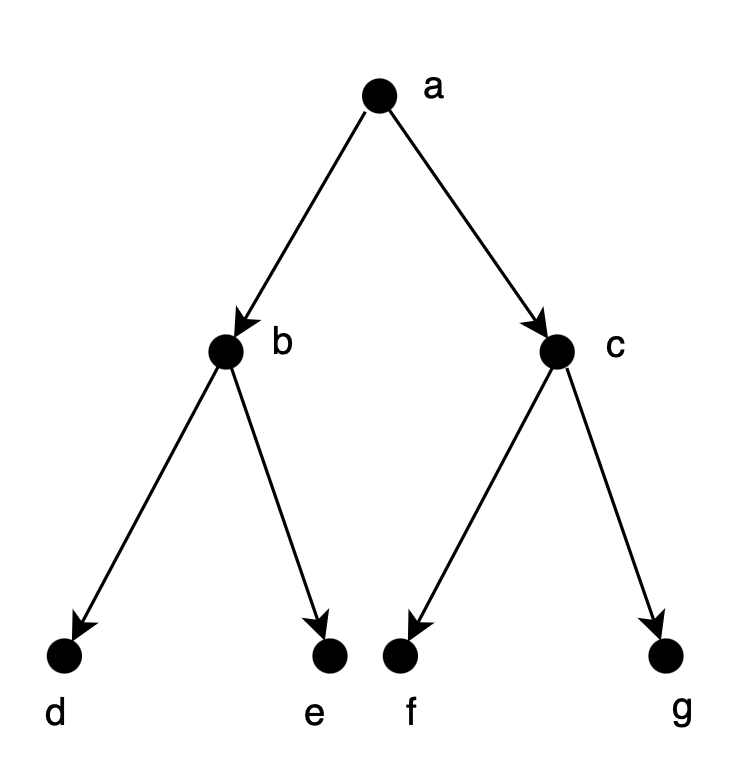
Gli alberi si usano per rappresentare informazioni organizzate in modo gerarchico, ad esempio l’albero genealogico di una famiglia, l’organizzazione di una azienda, la classificazione di piante ed animali, o in informatica per organizzare un filesystem. In generale sono utili in tutti i problemi in cui si ha bisogno di costruire un partizionamento dei dati, per semplificarne e/o renderne più veloce l’accesso e l’ordine.
Gli alberi hanno una specifica nomenclatura tecnica. Il nodo b è definito parent (padre) del nodo d, detto son (figlio). Il nodo da cui parte tutto l’albero (in questo caso a) viene chiamato root (radice) mentre il nodo terminale senza figli viene chiamato leaf (foglia), ad esempio e. L’arco che collega un nodo con un altro viene chiamato branch (ramo).
Gli alberi sono classificati per il numero di figli massimo che può avere un nodo. Gli alberi con nodi con 2 figli sono chiamati binari, quelli con 3 figli ternari, e così via. E’ importante osservare che non è detto che un albero debba essere completo, ovvero che tutti i nodi fino alle foglie abbiano lo stesso numero di figli, come nell’albero della figura sotto indicata.
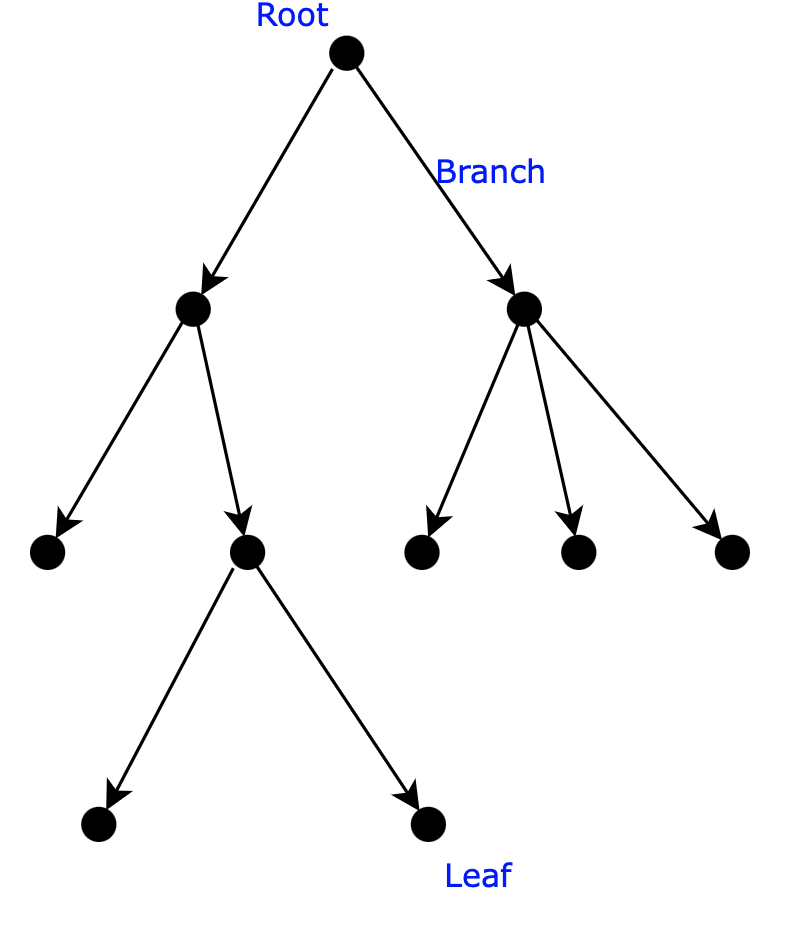
Viene definito path (cammino) il percorso che parte dalla radice e raggiunge una foglia attraverso un insieme di numeri intermedi. Viene definita profondità il cammino più lungo dalla radice alla foglia più lontana. Viene definita invece ampiezza il numero delle foglie totali.
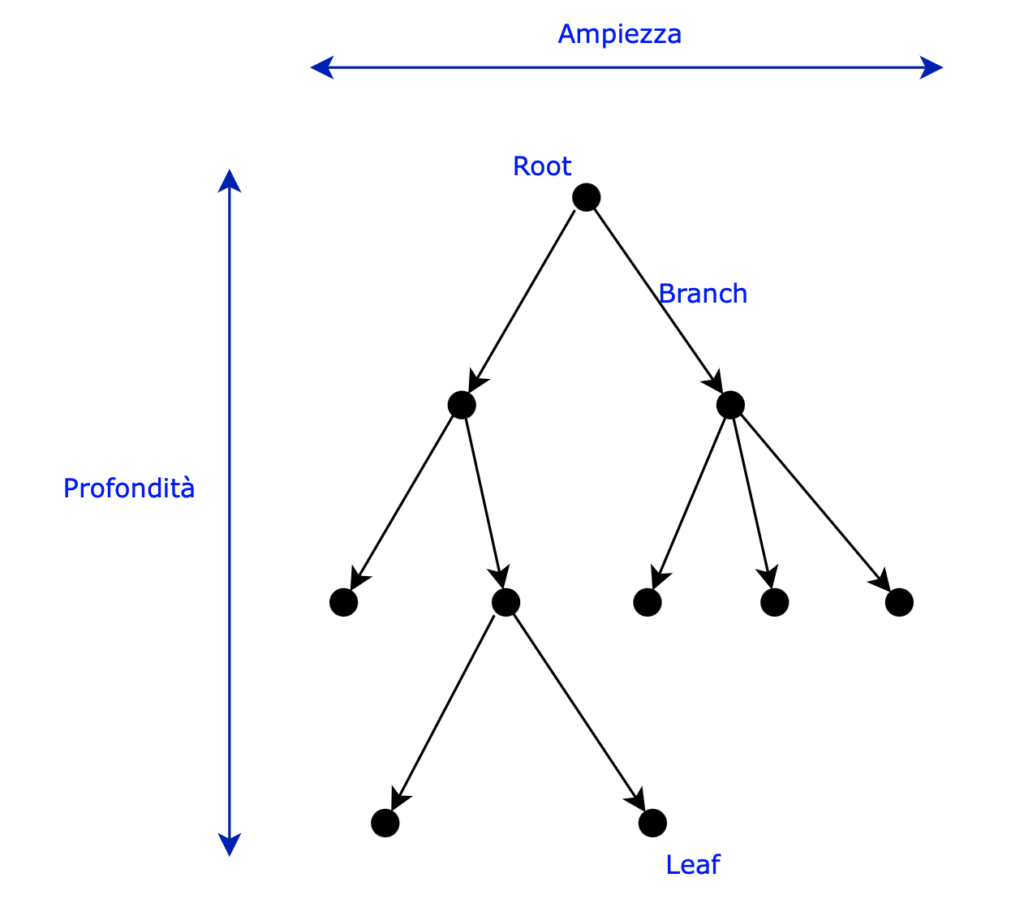
Alberi in C/C++
A livello di codice ci concentreremo sugli alberi binari e ci eserciteremo su di questi. Per rappresentare un albero binario in C/C++ si utilizza generalmente una struttura come la seguente:
struct Node {
int value;
Node* left;
Node* right;
};Naturalmente a seconda delle applicazioni, il nodo potrà contenere anzichè un semplice valore int qualsiasi combinazione di attributi, come qualsiasi struct.
Tornando ad un albero binario di valori interi una prima applicazione pratica di un albero binario è quella di usarlo ordinare una lista di valori generati casualmente.
#include <iostream>
#include <cstdlib>
using namespace std;
struct Node {
int value;
Node* left;
Node* right;
};
Node* insert(Node* node, int value) {
if (node == NULL) {
cout << "Inserisco valore " << value << endl;
node = new Node;
node->value = value;
} else {
if (node->value > value) {
cout << "Creo nodo a sx" << endl;
node->left = insert(node->left, value);
} else {
cout << "Creo nodo a dx" << endl;
node->right = insert(node->right, value);
}
}
return node;
}
int main()
{
srand(time(NULL));
int n;
cout << "Inserisci n:";
cin >> n;
int list[n];
Node* root = NULL;
for (int i=0; i<n; i++) {
list[i] = rand() % 50;
root = insert(root, list[i]);
}
visit_in_order(root);
return 0;
}Vediamo in dettaglio il codice:
- la funzione insert è una funzione ricorsiva con la seguente logica:
- se il nodo corrente è nullo, allora inserisce il valore;
- se il nodo corrente non è nullo, E il valore da inserire è inferiore, richiama se stessa sul nodo di sinistra
- se il nodo corrente non è nullo, E il valore da inserire è inferiore, richiama se stessa sul nodo di sinistra
- come si può vedere l’albero che si va a creare, avrà, per ogni nodo, tutti i nodi figli con valore inferiore a sinistra e tutti i nodi figli con valore superiore a destra.

- Come si può vedere dall’esempio l’albero, a seconda dell’ordine in cui i valori che vengono inseriti può assumere varie forme, non necessariamente simmetriche.
- La complessità computazionale di un ordinamento con l’albero binario è O(n*log(n)) in quanto è necessario scorrere tutta la lista da inserire (complessità n) e poi inserire i valori nell’albero tramite una ricerca della posizione prendendo di volta in volta il ramo a destra o sinistra. Nel caso non ottimale (ad esempio se partiamo da una lista ordinata) la complessità può diventare anche O(n2)
- la funzione visit_in_order visita l’albero ricostrendo la sequenza di valori ordinata: prima i valori a sinistra del nodo (ricorsivamente) poi il valore del nodo, poi i valori a destra (ricorsivamente).
void visit_in_order(Node* node) {
if (node != NULL) {
visit_in_order(node->left);
cout << node->value << endl;
visit_in_order(node->right);
}
}Se lo applichiamo all’esempio sopra indicato appare subito evidente che i numeri vengono visualizzati in ordine crescente, perché rispettiamo la stessa regola con cui sono stati inseriti, ovvero che localmente per ogni nodo dell’albero, abbiamo a sinistra valori più piccoli del nodo corrente, ed a destra valori più grandi.
Gli alberi di questo tipo vengono chiamati BST (Binary Search Tree, alberi binari di ricerca) perché il loro utilizzo principale è quello di essere utili per ricercare un valore in una lista. La complessità di questa operazione è infatti O(log(n)) in quanto ad ogni livello dell’albero dimezziamo il numero di nodi da visitare. Come per la visita tuttavia questo è il caso ottimale, se l’albero è completamente sbilanciato il tempo di accesso diventa lineare cioè O(n).
Profondità ed ampiezza di un albero
La profondità di un albero è il cammino dalla radice alla foglia più lontana.
int max_depth(Node *node, int deep, int max) {
if (node->left == NULL && node->right == NULL) {
if (max < deep) {
max = deep;
}
}
if (node->left != NULL) {
max = max_depth(node->left, deep+1, max);
}
if (node->right != NULL) {
max = max_depth(node->right, deep+1, max);
}
return max;
}L’ampiezza è invece il numero di foglie dell’albero.
int breadth(Node *node, int count) {
if (node->left == NULL && node->right == NULL) {
count = count+1;
}
if (node->left != NULL) {
count = breadth(node->left, count);
}
if (node->right != NULL) {
count = breadth(node->right, count);
}
return count;
}Bilanciare un albero
Come abbiamo visto sopra, un albero binario di ricerca può diventare fortemente sbilanciato. Ovvero, avere una profondità molto differente tra foglie differenti. Tecniche avanzate per risolvere questo problema in modo computazionalmente efficiente consistono nell’utilizzare un tipo speciale di alberi binari, detti alberi RB (Red Black, rosso neri) che per la sua complessità non verrà trattato qui. Un modo più semplice (ma più costoso computazionalmente) è invece quello di generare un albero normale, e poi da questo generare una lista ordinata. Da questa è poi possibile creare un albero bilanciato in modo ricorsivo prendendo l’elemento mediano della lista ed inserirlo in un nuovo albero da zero, e poi procedere ricorsivo con la prima metà e la seconda metà.
Il codice per realizzarlo è lasciato come esercizio.
